Excel NORMSINV (Sadržaj)
- Uvod u Excel NORMSINV
- Kako koristiti NORMSINV formulu u Excelu?
Uvod u Excel NORMSINV
Funkcija inverzne normalne kumulativne raspodjele u excelu je važan alat koji vraća inverznu normalnu kumulativnu raspodjelu za određenu vrijednost vjerojatnosti, tj. Obično vraća inverziju standardne normalne kumulativne distribucije (koja ima vrijednost nula i standardno odstupanje od jedne) Funkcija NORM.S.INV prvi put je uvedena u Microsoftovoj verziji excel 2010, koja je ažurirana verzija NORMSINV funkcije u excelu 2013 i najnovijoj verziji. NORMSINV funkcija uglavnom se koristi u analizi duga i financija.
Sintaksa programa Excel NORMSINV

Argument:
Vjerojatnost - koja nije ništa drugo nego vjerojatnost odgovara normalnoj distribuciji.
Kako koristiti NORMSINV formulu u Excelu?
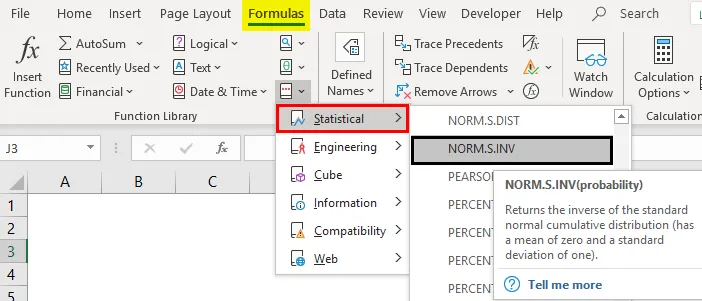
U Microsoftu excel ugrađena funkcija NORMSINV kategorizirana je prema statističkoj funkciji koja je prikazana na slici dolje (gdje će izračunati inverziju normalne kumulativne raspodjele za određenu vjerojatnost).
- Idite na izbornik formula.
- Kliknite Više funkcija kao što je prikazano na snimci zaslona.

- Odaberite kategoriju statistika pod kojom ćemo pronaći funkciju NORM.DIST kao što je prikazano u nastavku.
Primjer br. 1 - Korištenje NORM.DIST i NORMSINV
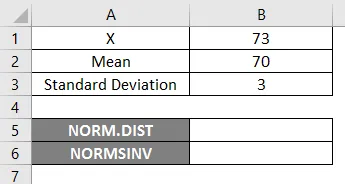
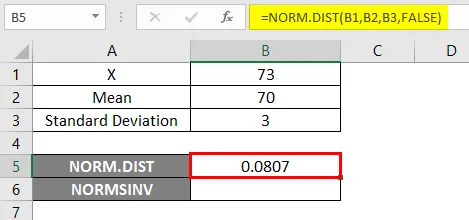
Kako bismo koristili funkciju NORM.DIST, započnimo s jednostavnim primjerom gdje trebamo saznati studentske ocjene, pretpostavimo da imamo razredni ispit s prosječnom ocjenom 70, tj. Mu = 70, a klase standardno odstupanje su 3 boda, tj. Sigma = 3 ovdje moramo otkriti kolika je vjerojatnost da su studenti dobili ocjene 73 ili niže, tj. P (X <= 73). Pa da vidimo kako saznati vjerojatnost pomoću funkcije NORM.DIST.
- X = 3
- Srednja = 70
- Standardno odstupanje = 3
- Primijenite funkciju NORM.DIST na sljedeći način.
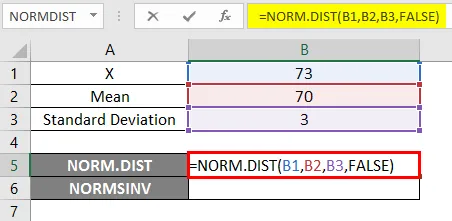
- Primijenimo li gornju NORM.DIST funkciju, dobit ćemo vjerojatnost 0, 0807.
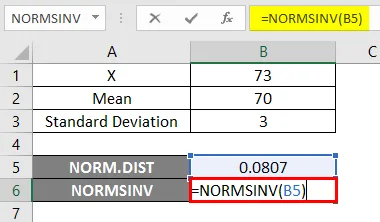
- Sada primijenite NORMSINV funkciju da biste saznali obrnuto normalnu kumulativnu raspodjelu kao što je prikazano u nastavku.
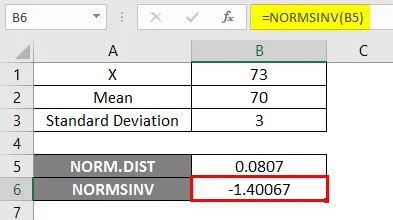
Rezultat -
Na donjem rezultatu možemo vidjeti da smo dobili negativne vrijednosti -1.40067 za datu vjerojatnost, tj. Obratnu normalnu kumulativnu raspodjelu.
Primjer br. 2 - Srednje i tačno standardno odstupanje
Pogledajmo još jedan primjer s podacima na temelju krivulje, tako da možemo upoznati srednju i točnu standardnu devijaciju.
- Srednja vrijednost = 7
- Standardno odstupanje = 1.3
- Standardni porast odstupanja kao -3

- Da bismo dobili krivulju zvona, moramo dodati 0, 1 dodatak standardnom odstupanju gdje su podaci prikazani dolje.
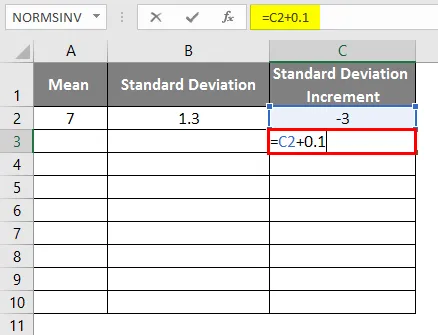
- Nakon primjene formule rezultat je kao što je prikazano u nastavku.
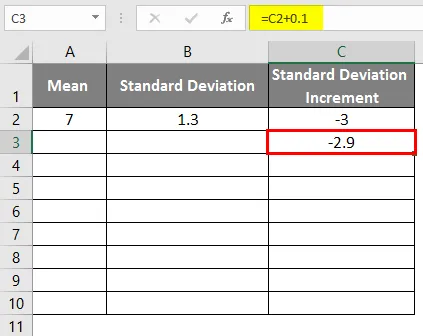
- Povucite vrijednosti kako bismo dobili više vrijednosti dok ne dobijemo pozitivne vrijednosti, tako da ćemo dobiti lijevu krivulju.
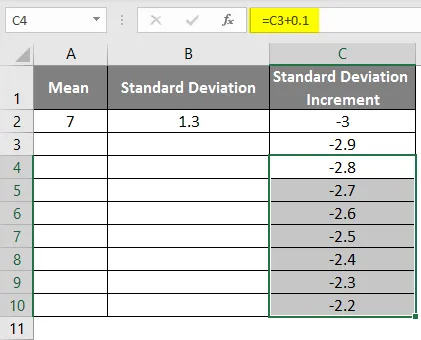
- Da bismo dobili desnu krivulju, moramo primijeniti formulu kao = srednje-standardno odstupanje * 3, tako da ćemo dobiti točne krivulje.
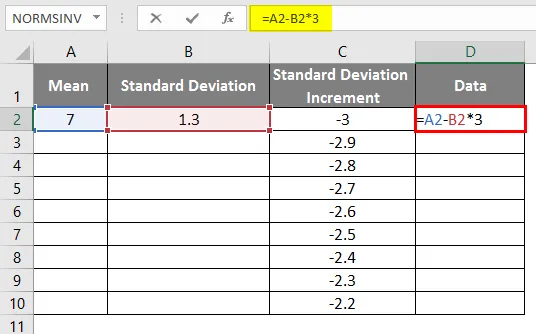
- Nakon korištenja formule rezultat je prikazan dolje.
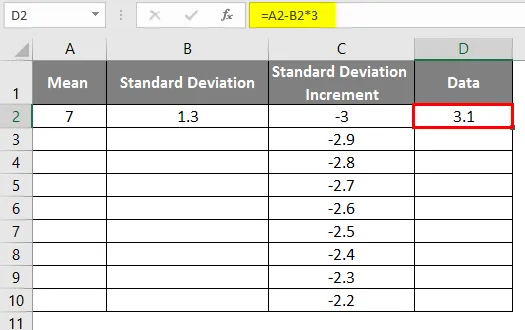
- Kao što je u gornjim podacima za porast standardne devijacije za dobivanje lijeve krivulje vrijednosti smo povećali za 0, 1
- Isti se scenarij upotrebljava primjenom formule kao = 3.1 + STANDARDNI RAZVOJ / 10 za dobivanje povećanja krivulje 0, 1
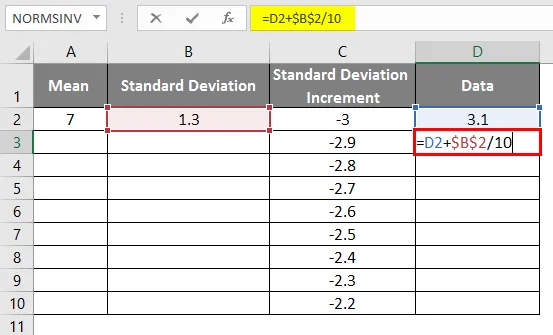
- Nakon korištenja formule rezultat je prikazan dolje.

- Povucite vrijednosti da biste dobili točan rezultat koji je prikazan na slici ispod.
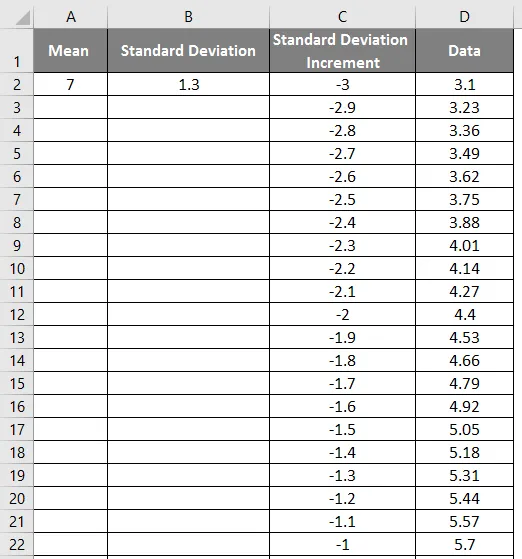
- Sada primijenite normalnu funkciju raspodjele s formulom = NORM.DIST (DATA vrijednost, srednja vrijednost, standardna devijacija, false).
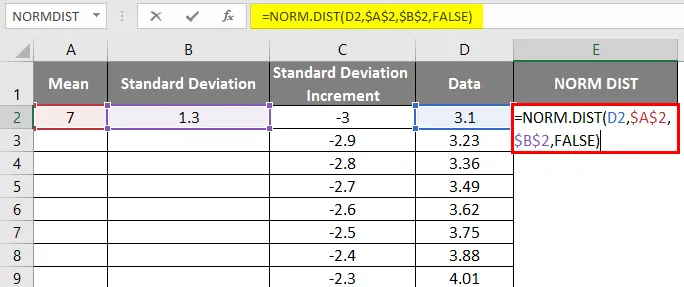
- Dobiveni rezultat ćemo dobiti na sljedeći način.
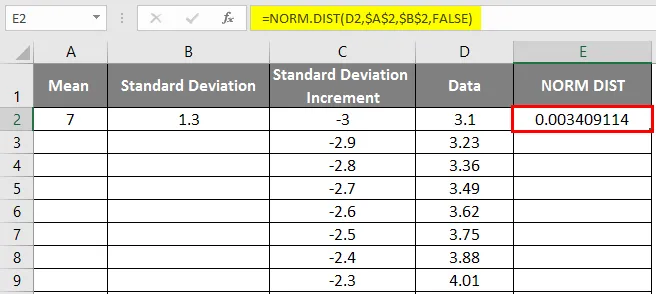
- Povucite vrijednosti kako biste dobili točan rezultat koji je prikazan u nastavku.
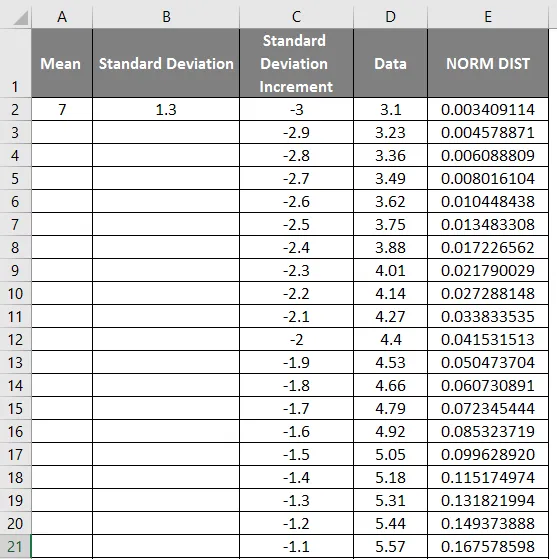
- Kao što vidimo na gornjem snimku zaslona, izračunali smo NORMALnu distribuciju od srednje i standardne devijacije. Sada da vidimo što će biti obrnuto NORMALNOM raspodjelom primjenom NORMSINV-a koji je prikazan u nastavku.
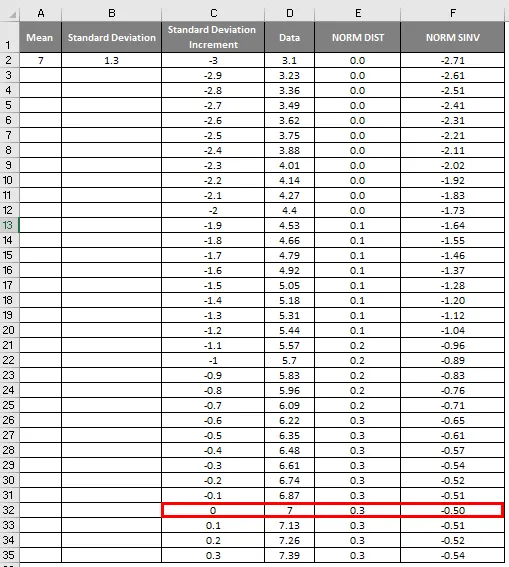
- Ovdje možemo vidjeti da vrijednost Zero (0) ima standardno odstupanje kao 7.

Primjenom raštrkanog grafikona pogledajte kako izgledaju lijeva i desna krivulja.
- Prvo odaberite podatke i stupac Normal.
- Idite na karticu Umetanje i odaberite raštrkani graf na sljedeći način.
- Dobit ćemo graf krivulje ispod, kao što je prikazano u nastavku.
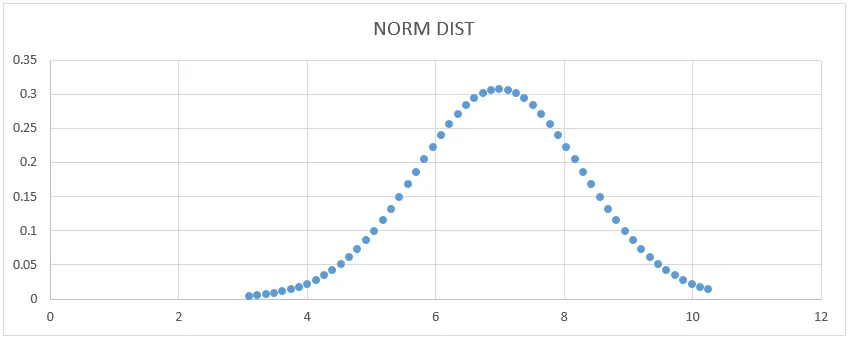
Ovdje možemo vidjeti da Srednja vrijednost 7 ima standardni oblik odstupanja gdje to možemo pokazati crtanjem ravne linije koja će ga predstavljati.
- Srednja vrijednost = 7
- 1 - Standardno odstupanje ukazuje na 68% podataka.
- 2 - Standardno odstupanje označava 95% podataka.
- 3 - Standardno odstupanje ukazuje na 99, 7% podataka.
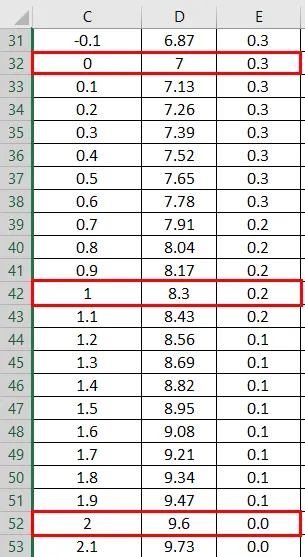
Grafikon normalne distribucije:
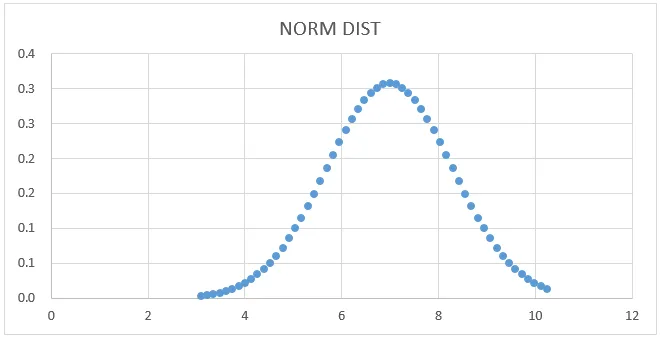
NORMSINV Grafikon:
Sada s gornje slike odaberite stupac podataka i NORM SINV da biste dobili donji grafikon kako slijedi.
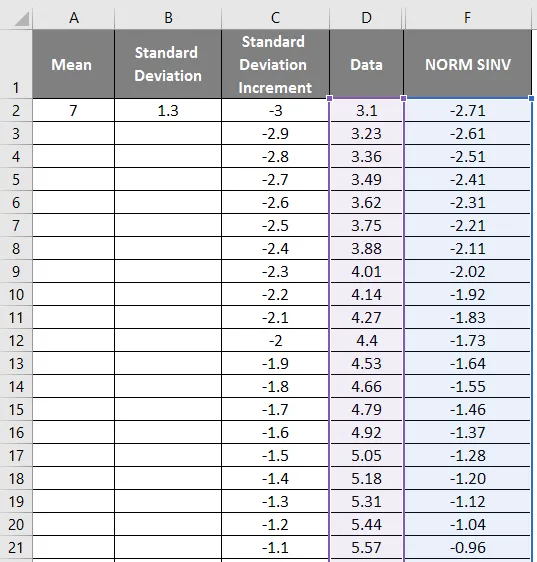
- Prvo odaberite podatke i stupac Normal.
- Idite na karticu Umetanje i odaberite raštrkani graf.
- Dobit ćemo graf ispod koji je prikazan na slici ispod.
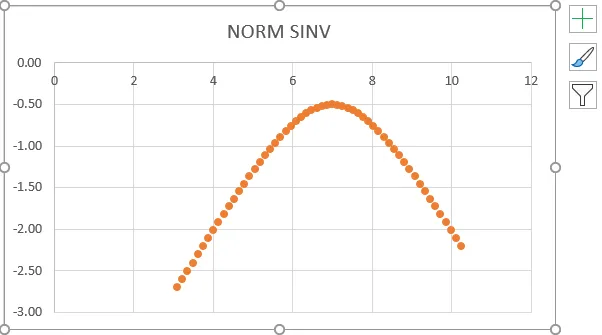
- Iz gornjeg snimka zaslona možemo vidjeti da smo dobili točan obratni smjer normalne raspodjele koji prikazuje istu vrijednost vrijednosti prikazanu dolje.

Primjer 3 - Konfiguriranje lijeve i desne krivulje
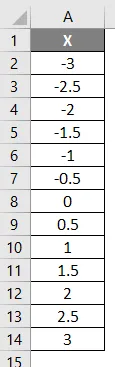
U ovom ćemo primjeru konfigurirati lijevu i desnu krivulju koristeći normalnu distribucijsku funkciju. Razmotrite dolje prikazane podatke, kako su dolje prikazani, gdje x ima negativne vrijednosti i povećava se na pozitivne vrijednosti.
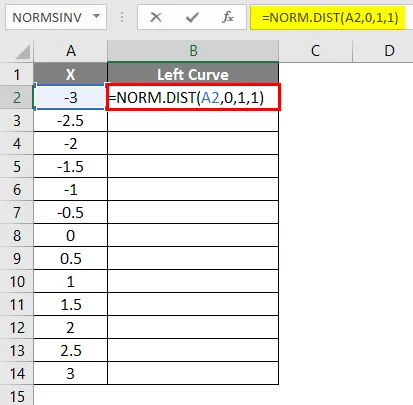
- Primijenite formulu = NORM.DIST (A2, 0, 1, 1).
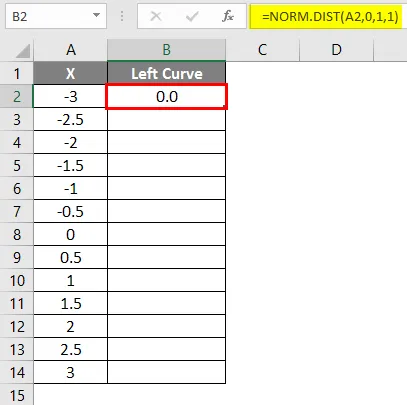
- Nakon primjene formule rezultat je prikazan dolje.
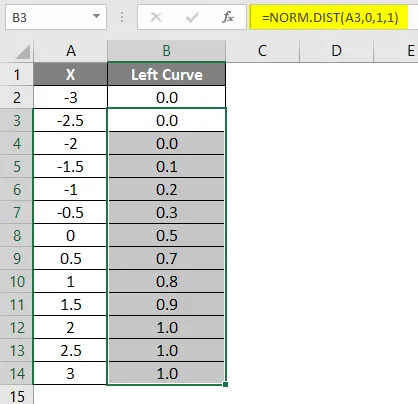
- Povucite formulu u drugim ćelijama.
- Primijenite formulu = 1-B2 .
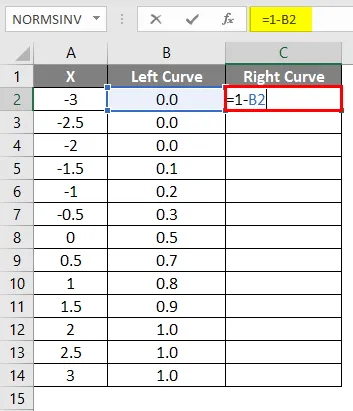
- Nakon primjene formule rezultat je prikazan dolje.
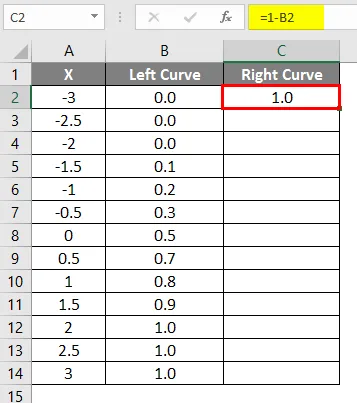
- Povucite istu formulu u ostalim ćelijama.
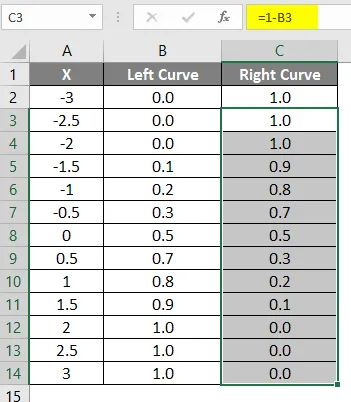
Rezultat gore primijenjene formule prikazan je dolje.
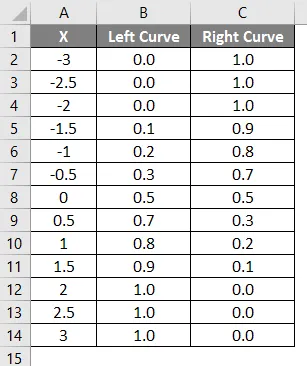
- Vrijednosti lijeve krivulje izračunate su primjenom formule NORMALNA DISTRIBUCIJA postavljanjem kumulativne vrijednosti kao True i NORMSINV je izračunata korištenjem lijeve krivulje.
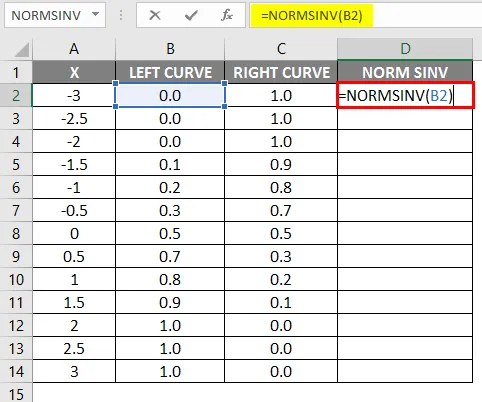
- Nakon primjene formule rezultat je prikazan dolje.
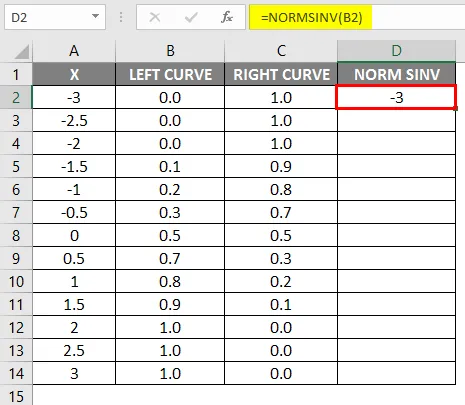
- Povucite istu formulu u ostalim ćelijama.
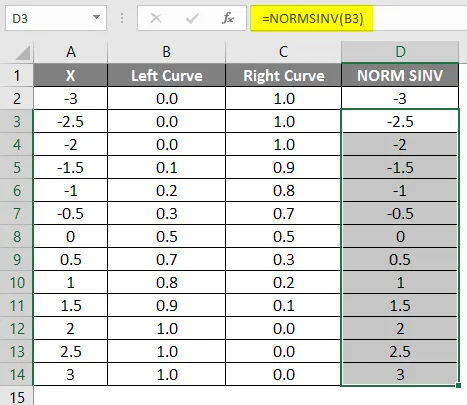
Kao što vidimo da smo za NORMSINV dobili istu vrijednost koja nije ništa drugo nego obrnuta normalna distribucija. Na isti način dobit ćemo vrijednost desne krivulje izračunavanjem vrijednosti 1-lijeve krivulje. U sljedećem koraku ćemo provjeriti kako ćemo pomoću visjenog grafikona dobiti visinu x.
- Odaberite lijevi stupac lijeka i desni krivulju.
- Idite na umetanje izbornika.
- Odaberite raštrkani graf na sljedeći način.
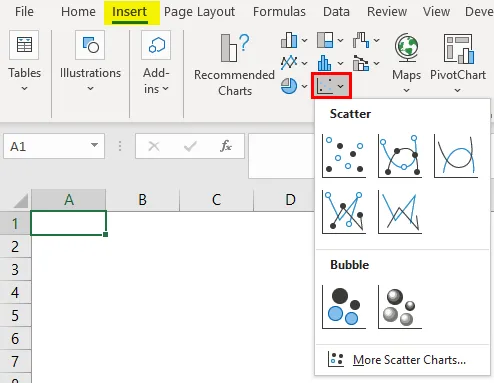
Dobit ćemo grafikon u nastavku kao što je prikazano u nastavku.
NORM SINV Graf:
Na donjem grafikonu možemo vidjeti da lijeva krivulja NORM DISTRIBUTIJE ima točno podudaranje za (0, 0, 5) koja leži u središtu crte gdje ćemo dobiti isti graf ako se prijavimo za NORMDIST.
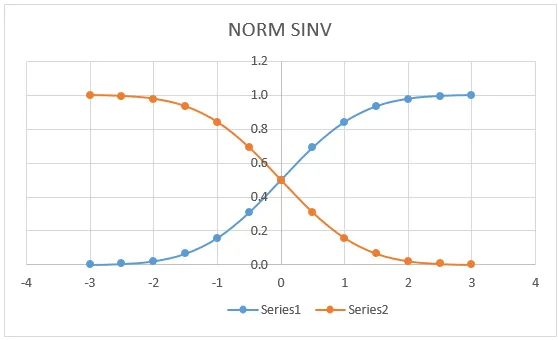
Ovdje na gornjem grafikonu vrlo jasno se vidi da smo dobili točnu sredinu u središnjoj točki koja označava:
- X = 0
- Lijeva krivulja = 0, 5
- Desna krivulja = 0, 5
Prikazali smo ga da vidimo NORMSINV vrijednosti u grafičkom formatu kao što je prikazano u nastavku.
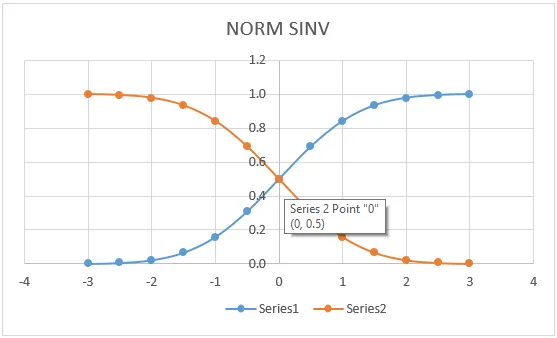
Stvari koje treba zapamtiti o Excelu NORMSINV
- #vrijednost! Do pogreške dolazi kada je zadani argument ne numerička ili logička vrijednost.
- U funkciji normalne distribucije obično dobivamo #NUM! pogreška zbog argumenta standardnog odstupanja je manja ili jednaka nuli.
Preporučeni članci
Ovo je vodič za Excel NORMSINV. Ovdje smo raspravljali o tome kako koristiti NORMSINV u Excelu zajedno s praktičnim primjerima i besplatnim Excel predložakom. Možete i pregledati naše druge predložene članke -
- Kako koristiti okvir s imenima u Excelu?
- Rad s Matrix-om u Excelu
- Što ako analiza u Excelu
- NPV formula u Excelu