
Uvod u Razvrstavanje spajanja u JavaScript
Algoritmi sortiranja vrlo su važni u računalnoj znanosti. Rezultat sortiranja je raspoređivanje elemenata popisa prema određenom redoslijedu (uzlazno ili silazno). Spajanje sortiranja u JavaScriptu jedan je od najučinkovitijih dostupnih algoritama sortiranja, jer se temelji na konceptu dijeljenja i osvajanja. Kao što ime sugerira, prvo podijelite veći problem na male probleme nego rješavajte manje probleme da biste riješili veći problem. Konceptualno, Spajanje sortiranja je kombinacija dvaju osnovnih algoritama zvanih MERGE i MERGE_SORT.
koja djeluje na sljedeći način:
- Podijelite nesvrstani popis na n broj potpopisa s jednom stavkom (n je ukupni broj elemenata u poništenom popisu).
- Ponavljano spajanje popisa u poredane popisa dok ne postoji samo jedan popis sortiran.
Primjena vrste spajanja u JavaScript-u
MERGE algoritam slijedi postupak kombiniranja dva sortirana popisa u jedan sortirani popis.
Primjer: Pretpostavimo da postoje dva popisa, tj. Popis 1 (1, 5, 3) i Popis 2 (7, 2, 9).
1. Prvo sortirajte oba popisa.
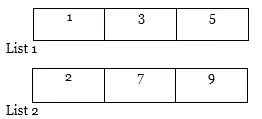
Sada ćemo vidjeti i primijeniti E tehniku na njoj.
2. Zatim ćemo stvoriti novi popis veličine x + y gdje je x broj elemenata u Popisu 1, a y je broj elemenata u Popisu 2.

U našem slučaju x = 3 i y = 3, pa je x + y = 6.
3. Sada imamo dva pokazivača.
Prvi pokazivač usmjeren na prvo mjesto popisa 1 i drugi pokazivač koji upućuje na prvi položaj popisa 2.

4. Zatim ćemo usporediti vrijednost oba pokazivača. Pokazivač manje vrijednosti, kopirajte taj element u Listu 3 i pomaknite pokazivač desno od popisa s manjom vrijednošću i rezultatom popisa (tj. Popis 1 i Popis 3)

5. Slično, izvedite korak 4 iznova i iznova.

Daljnje putovanje… ..
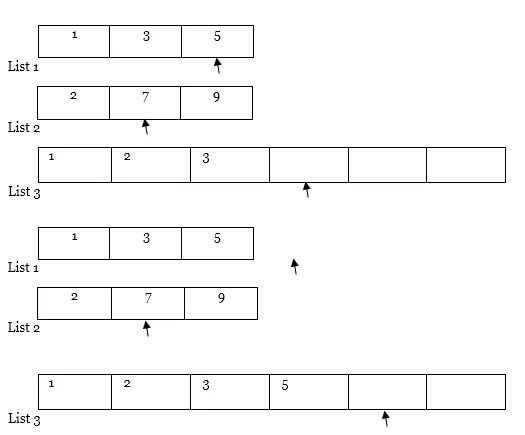
Napomena : Ako se jedan od popisa (tj. Popis 1 ili popis 2) u potpunosti pređe kao u slučaju, kopirajte cijeli sadržaj drugog popisa s pokazivača na popis rezultata (tj. Popis 3) na sljedeći način.

pseudokod
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
Algoritam MERGE_SORT podijeli zadani nesortirani popis na minimalnu veličinu, a zatim poziva algoritam MERGE da kombinira popis u novi poredani popis.
pseudokod
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Primjer
Ovdje pratimo implementaciju Razvrstavanje spajanja od vrha prema dolje. Počinje od vrha i nastavlja se prema dolje, sa svakim rekurzivnim zaokretom postavlja isto pitanje „Što je potrebno učiniti da bi se popis razvrstao?“, A odgovor je „Podijelite popis na dva, napravite rekurzivni poziv i spojite rezultati”.
Kôd u Javascriptu
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
Glavna funkcija sortiranja spajanja podijelit će zadani popis na manje liste u svakoj iteraciji rekurzivnog poziva. Ne zaboravite da rekurzija zahtijeva osnovno stanje kako bi se izbjegla beskonačna rekurzija. U našem slučaju imamo:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
Nakon što smo postavili osnovni uvjet za rekurziju, tada ćemo identificirati srednji indeks za podjeljenje zadanog popisa na lijevi i desni podpopis, kao što možete vidjeti gore na primjeru dijagrama. Zatim trebamo spojiti lijevi potpopis i desni potpopis koji ćemo sada gledati. U gornjoj funkciji spajanja trebamo osigurati da sortiramo sve elemente na lijevom potpopisu i desnom podpopisu. popis. Način na koji ćemo to učiniti je pomoću petlje. U petlji while uspoređivat ćemo jedan po jedan element u lijevom potpopisu i element u desnom podpopisu. Manji od dva možemo gurnuti u popis rezultata i prema tome pomaknuti pokazivač lijevog podpisa i desnog potpopisa. Na kraju, moramo povezati popis rezultata. Ovo je veoma važno! Ako ovdje ne učinimo ovaj posljednji korak, na kraju ćemo imati nepotpun popis elemenata jer uvjet petlje neće uspjeti kad bilo koji od dva pokazivača dođe do kraja.
Izlaz:

Svojstva sortiranja spajanja
- Razvrstavanje spajanja stabilno je jer isti element u nizu održava svoje izvorne položaje u odnosu jedan prema drugom.
- Razvrstavanje spajanja nije na mjestu jer se tijekom spajanja stvara kopija cjelokupnog popisa. Zbog toga je složenost prostora (O (n)) ovog algoritma zapravo veća od ostalih i ne treba ga koristiti u složenim problemima u kojima je prostor vrhunski.
- Ukupna vremenska složenost sortiranja Spajanja je O (nLogn). To je učinkovitije kao što je u najgorem slučaju i vrijeme izvođenja je O (nlogn).
Zaključak
Najbolje su složite, najsloženije i prosječne vremenske složenosti su iste što ga čini učinkovitijim algoritmom. Djeluje brže od ostalih tehnika sortiranja. Vrsta spajanja može se primijeniti na datoteke bilo koje veličine. Vrlo je paralelizabilna zbog metode dijeljenja i osvajanja. Da biste razvili snažne osnove u računarskim znanostima, savjetujemo vam da temeljito razumijete različite algoritme sortiranja.
Preporučeni članak
Ovo je vodič za spajanje sortiranja u JavaScript-u. Ovdje smo raspravljali o Uvođenju u spajanje sortiranja u JavaScript i implementaciji zajedno sa Svojstvima. Možete i proći naše druge predložene članke da biste saznali više -
- JavaScript matematičke funkcije
- Uvod u JavaScript
- Najbolji okviri Javascript
- JavaScript alati
- Top 6 algoritma za razvrstavanje u JavaScript