Razlika između linearne regresije i logističke regresije
Sljedeći članak Linearna regresija vs logistička regresija pruža najvažnije razlike između obojice, ali prije nego što ćemo vidjeti što znači regresija?
Regresija
Regresija je u osnovi statistička mjera kojom se utvrđuje jačina veze između jedne ovisne varijable, tj. Izlaza Y i niza drugih neovisnih varijabli, tj. X 1, X 2 i tako dalje. Regresijska analiza u osnovi se koristi za predviđanje i predviđanje.
Što je linearna regresija?
Linearna regresija je algoritam koji se temelji na nadziranoj domeni strojnog učenja. Nasljeđuje linearni odnos između svojih ulaznih varijabli i pojedinačne izlazne varijable gdje je izlazna varijabla u prirodi kontinuirana. Koristi se za predviđanje vrijednosti izlaza, recimo Y iz ulaza, recimo X. Kada se smatra samo jedan ulaz, to se zove jednostavna linearna regresija.
Može se razvrstati u dvije glavne kategorije:
1. Jednostavna regresija
Načelo rada: Glavni cilj je pronaći jednadžbu ravne linije koja najbolje odgovara uzorkovanim podacima. Ova jednadžba algebrično opisuje odnos između dvije varijable. Ravna linija koja najbolje pristaje naziva se regresijska linija.
Y = β 0 + β 1 X
Gdje,
β predstavlja značajke
β 0 predstavlja presretanje
β 1 predstavlja koeficijent svojstva X
2. Multivarijabilna regresija
Koristi se za predviđanje povezanosti između više nezavisnih varijabli i jedne ovisne varijable. Regresija s više od dvije neovisne varijable temelji se na uklapanju oblika u konstelaciju podataka na višedimenzionalnom grafu. Oblik regresije treba biti takav da minimizira udaljenost oblika od svake podatkovne točke.
Model linearnog odnosa može se matematički predstaviti na sljedeći način:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Gdje,
β predstavlja značajke
β 0 predstavlja presretanje
β 1 predstavlja koeficijent svojstva X1
β n predstavlja koeficijent obilježja X n
Prednosti i nedostaci linearne regresije
U nastavku su navedene prednosti i nedostaci:
prednosti
- Zbog svoje jednostavnosti, široko se koristi modeliranje za predviđanja i zaključke.
- Usmjeren je na analizu podataka i predobradu podataka. Dakle, bavi se različitim podacima bez muke oko detalja modela.
Nedostaci
- Učinkovito djeluje kada se podaci normalno distribuiraju. Stoga se za učinkovito modeliranje mora izbjegavati kolinearnost.
Što je logistička regresija?
To je oblik regresije koji omogućava predviđanje diskretnih varijabli mješavinom kontinuiranih i diskretnih prediktora. Rezultat je jedinstvena transformacija ovisnih varijabli koja utječe ne samo na postupak procjene, već i na koeficijente neovisnih varijabli. Bavi se istim pitanjem koje ima višestruka regresija, ali bez distribucijskih pretpostavki o prediktorima. U logističkoj regresiji varijabla ishoda je binarna. Svrha analize je procijeniti učinke više objašnjivih varijabli, koje mogu biti numeričke ili kategoričke ili oboje.
Vrste logističke regresije
Ispod su dvije vrste logističke regresije:
1. Binarna logistička regresija
Koristi se kada je ovisna varijabla dihotomna tj. Poput stabla s dvije grane. Koristi se kada je ovisna varijabla neparametarska.
Koristi se kad
- Ako nema linearnosti
- Postoje samo dvije razine ovisne varijable.
- Ako je multivarna normalnost dvojbena.
2. Multinomalna logistička regresija
Multinominalna logistička regresijska analiza zahtijeva da neovisne varijable budu metričke ili dihotomne. Ne daje nikakve pretpostavke linearnosti, normalnosti i homogenosti varijance za neovisne varijable.
Koristi se kada ovisna varijabla ima više od dvije kategorije. Koristi se za analizu odnosa između ne metričke ovisne varijable i metričkih ili dihotomskih neovisnih varijabli, zatim uspoređuje više skupina kombinacijom binarnih logističkih regresija. Na kraju, on pruža skup koeficijenata za svaku od dvije usporedbe. Koeficijenti za referentnu skupinu su sve nule. Konačno, predviđanje se vrši na temelju najveće rezultirajuće vjerojatnosti.
Prednost logističke regresije: To je vrlo učinkovita i široko korištena tehnika jer ne zahtijeva mnogo računskih resursa i ne zahtijeva podešavanje.
Nedostatak logističke regresije: Ne može se koristiti za rješavanje nelinearnih problema.
Usporedba između linearne regresije i logističke regresije (Infographics)
Ispod je top 6 razlike između linearne regresije i logističke regresije 
Ključna razlika između linearne regresije i logističke regresije
Razgovarajmo o nekim glavnim ključnim razlikama između linearne regresije i logističke regresije
Linearna regresija
- To je linearni pristup
- Koristi ravnu crtu
- Ne može preuzeti kategorijske varijable
- Mora zanemariti opažanja s nedostajućim vrijednostima numeričke neovisne varijable
- Izlaz Y je dan kao
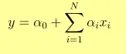
- 1 jedinica povećanja x povećava Y za α
Prijave
- Predviđanje cijene proizvoda
- Predviđanje rezultata u utakmici
Logistička regresija
- To je statistički pristup
- Koristi sigmoidnu funkciju
- Može uzeti kategoričke varijable
- Može donositi odluke čak i ako su prisutna zapažanja s nedostajućim vrijednostima
- Izlaz Y dan je kao, gdje je z dan kao
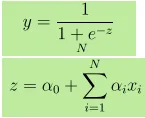
- Povećanje za 1 jedinicu u x povećava Y zabojem od α
- Ako je P vjerojatnost nekog događaja, tada je (1-P) vjerojatnost da se on neće dogoditi. Kvote uspjeha = P / 1-P
Prijave
- Predviđajući hoće li danas kiša ili ne.
- Predviđanje je li e-pošta neželjena pošta ili ne.
Tabela usporedbe linearne regresije i logističke regresije
Razgovarajmo o gornjoj usporedbi između linearne regresije i logističke regresije
|
Linearna regresija |
Logistička regresija |
| Koristi se za rješavanje regresijskih problema | Koristi se za rješavanje problema s klasifikacijom |
| Modelira odnos između ovisne varijable i jedne ili više nezavisnih varijabli | Predviđa vjerojatnost ishoda koja na izlazu može imati samo dvije vrijednosti bilo 0 ili 1 |
| Predviđeni izlaz je kontinuirana varijabla | Predviđeni izlaz je diskretna varijabla |
| Predviđeni izlaz Y može prelaziti 0 i 1 raspon | Predviđeni izlaz Y leži unutar 0 i 1 raspona |
 | 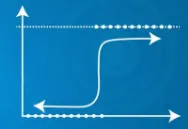 |
| Predviđeni izlaz Y može prelaziti 0 i 1 raspon | Predviđeni izlaz |
Zaključak
Ako značajke ne doprinose predviđanju ili su u velikoj međusobnoj korelaciji, to modelu dodaje buku. Dakle, značajke koje ne doprinose dovoljno modelu moraju biti uklonjene. Ako su neovisne varijable visoko povezane, to može uzrokovati problem multikolinearnosti, što se može riješiti pokretanjem zasebnih modela sa svakom neovisnom varijablom.
Preporučeni članci
Ovo je vodič za Linearnu regresiju i logističku regresiju. Ovdje smo razmotrili ključne razlike linearne regresije i logističke regresije s infografikom i tablicom usporedbe. Možete također pogledati sljedeće članke da biste saznali više -
- Znanost podataka vs vizualizacija podataka
- Strojno učenje i neuronska mreža
- Nadzirano učenje vs Duboko učenje
- Logistička regresija u R