Uvod u hijerarhijsko klasteriranje
- Nedavno je jedan od naših klijenata tražio da naš tim iznese spisak segmenata po redoslijedu važnosti unutar svojih kupaca kako bi ih ciljao da franšiziraju jedan od svojih novootvorenih proizvoda. Jasno je da samo segmentiranje korisnika pomoću djelomičnog grupiranja (k-znači, c-fuzzy) neće donijeti važan redoslijed tamo gdje hijerarhijsko grupiranje ulazi u sliku.
- Hijerarhijsko grupiranje razdvaja podatke u različite skupine na temelju nekih mjera sličnosti poznatih kao klasteri, a koji u osnovi cilja na izgradnju hijerarhije među klasterima. U osnovi je nekontrolirano učenje i odabir atributa za mjerenje sličnosti ovisan je o aplikaciji.
Hijerarhija podataka klastera
- Aglomerativno klasteriranje
- Podjela klastera
Uzmimo za primjer podatke, ocjene dobivene od 5 učenika kako bismo ih grupirali za nadolazeće natjecanje.
| Student | Marks |
| 10 | |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Aglomerativno klasteriranje
- Za početak, svaku težinu pojedinih točaka / elemenata ovdje smatramo klasterima i nastavljamo spajanjem sličnih točaka / elemenata kako bi formirali novi klaster na novoj razini dok nam ne ostane samo jedan klaster je pristup odozdo prema gore.
- Pojedinačna i potpuna veza dva su popularna primjera aglomerativnog grupiranja. Osim ove srednje veze i Centroidne veze. U jednom povezivanju spajamo u svakom koraku dva grozda, čija dva najbliža člana imaju najmanju udaljenost. U potpunom povezivanju spajamo se u najmanju udaljenost članova koji pružaju najmanju maksimalnu udvojenu udaljenost.
- Matrica blizine, To je jezgra za izvođenje hijerarhijskog grupiranja, koja daje udaljenost između svake točke.
- Napravimo matricu blizine za naše podatke dane u tablici, budući da izračunavamo udaljenost između svake točke s ostalim točkama, to će biti asimetrična matrica oblika n × n, u našem slučaju 5 × 5 matrica.
Popularna metoda za proračun udaljenosti su:
- Euklidijska udaljenost (u kvadratu)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Udaljenost na Manhattanu
dist((x, y), (a, b)) =|x−c|+|y−d|
Euklidska udaljenost se najčešće koristi, tu ćemo je koristiti i ići ćemo složenim povezivanjem.
| Student (Klasteri) | B | C | D | E | |
| 0 | 3 | 18 | 10 | 25 | |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Dijagonalni elementi matrice blizine uvijek će biti 0, jer će udaljenost između točke s istom točkom uvijek biti 0, stoga su dijagonalni elementi izuzeti iz razmatranja za grupiranje.
Ovdje je u iteraciji 1 najmanja udaljenost 3 stoga spajamo A i B u skupinu, a opet formiramo novu matricu blizine s klasterom (A, B) uzimanjem (A, B) točke klastera kao 10, tj. Maksimumom ( 7, 10) tako bi bila novoformirana matrica blizine
| klasteri | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
U iteraciji 2, 7 je minimalna udaljenost stoga spajamo C i E formirajući novi klaster (C, E), ponavljamo postupak koji slijedi u iteraciji 1 dok ne završimo s jednim klasterom, ovdje se zaustavljamo na iteraciji 4.
Čitav postupak je prikazan na slici ispod:
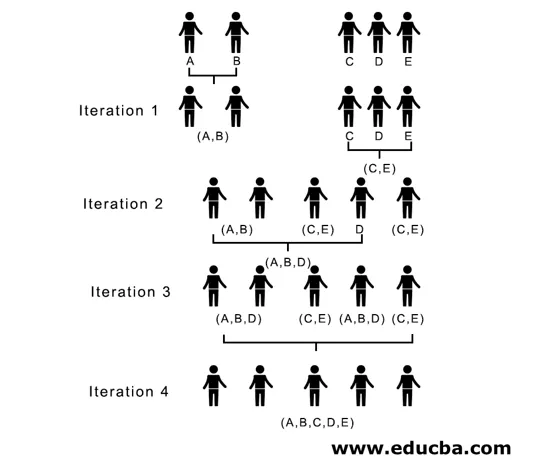
(A, B, D) i (D, E) su dva klastera formirana u iteraciji 3, na posljednjoj iteraciji koju vidimo možemo ostati s jednim klasterom.
2. Podjela klastera
Za početak, sve točke smatramo jedinstvenom grupom i razdvajamo ih na najveću udaljenost dok pojedinačnim točkama ne završimo kao pojedinačni klasteri (ne nužno da se možemo zaustaviti u sredini, ovisi o minimalnom broju elemenata koje želimo u svakom klasteru) na svakom koraku. To je upravo suprotno aglomerativnom grupiranju i to je pristup odozgo prema dolje. Podijeljeno grupiranje je način na koji se ponavlja k znači grupiranje.
Odabir između aglomerativnog i razdjelnog klasteriranja opet ovisi o aplikaciji, ali treba uzeti u obzir nekoliko točaka:
- Podjela je složenija od aglomerativnog grupiranja.
- Razdjelno grupiranje je učinkovitije ako ne stvorimo potpunu hijerarhiju do pojedinih podataka.
- Aglomerativno grupiranje donosi odluku uzimajući u obzir lokalne uzorke, ne uzimajući u obzir globalne obrasce koji se u početku ne mogu preokrenuti.
Vizualizacija hijerarhijskog klasteriranja
Super korisna metoda za vizualizaciju hijerarhijskog grupiranja koja pomaže u poslovanju je Dendogram. Dendogrami su strukture poput stabala koje bilježe redoslijed spajanja i rasjeda u kojima vertikalna linija predstavlja udaljenost između klastera, udaljenost između vertikalnih linija i udaljenost između klastera izravno je proporcionalan tj. Što je više udaljenosti što su klasteri vjerovatno različiti.
Pomoću dendograma možemo odrediti broj klastera, samo nacrtajmo liniju koja se presijeca s najdužom vertikalnom linijom na dendogramu, broj vertikalnih linija koje se presijecaju bit će broj klastera koji će se uzeti u obzir.
Ispod je primjer Dendogram.
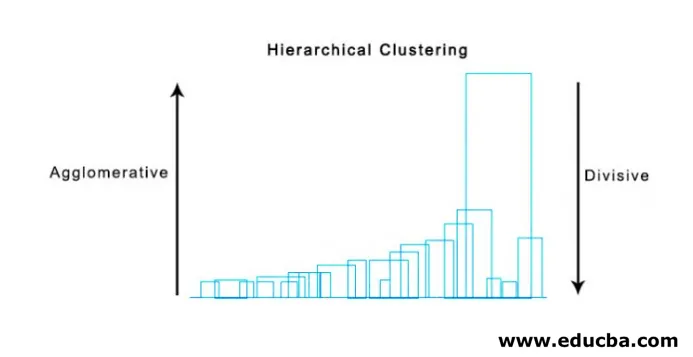
Postoje prilično jednostavni i izravni python paketi i njegove funkcije za izvršavanje hijerarhijskog grupiranja i crtanje dendograma.
- Hijerarhija od scipy.
- Cluster.hierarchy.dendogram za vizualizaciju.
Uobičajeni scenariji u kojima se koristi hijerarhijsko klasteriranje
- Segmentacija korisnika na marketing proizvoda ili usluga.
- Gradsko planiranje identificirati mjesta za izgradnju struktura / usluga / zgrada.
- Analiza društvenih mreža, na primjer, identificirati sve obožavatelje MS Dhonija koji oglašavaju njegov životopis.
Prednosti hijerarhijskog klasteriranja
Prednosti su dane u nastavku:
- U slučaju djelomičnog grupiranja poput k-sredstava, prije klasteriranja treba znati broj klastera, što u praktičnim primjenama nije moguće, dok u hijerarhijskom grupiranju nije potrebno prethodno znanje broja klastera.
- Hijerarhijsko grupiranje daje hijerarhiju, tj. Strukturu informativniju od nestrukturiranog skupa ravnih klastera vraćenog djelomičnim grupiranjem.
- Hijerarhijsko grupiranje je jednostavno implementirati.
- Donosi rezultate u većini scenarija.
Zaključak
Tip klasteriranja donosi veliku razliku u predstavljanju podataka, preferira se hijerarhijsko klasteriranje koje je informativnije i jednostavno za analizu nego djelomično grupiranje. A često je povezana s toplotnim kartama. Da se ne zaborave atributi odabrani za izračunavanje sličnosti ili različitosti, koji uglavnom utječu i na klastere i na hijerarhiju.
Preporučeni članci
Ovo je vodič za hijerarhijsko grupiranje. Ovdje ćemo raspravljati o uvodu, prednostima hijerarhijskog klasteriranja i uobičajenim scenarijima u kojima se koristi hijerarhijsko klasteriranje. Možete i proći kroz naše druge predložene članke da biste saznali više -
- Algoritam klastera
- Klasteriranje u strojnom učenju
- Hijerarhijsko klasteriranje u R
- Metode klasteriranja
- Kako ukloniti hijerarhiju u Tableauu?