Formula efektivne godišnje stope (Sadržaj)
- Formula
- Primjeri
- Kalkulator
Što je efektivna formula godišnje stope?
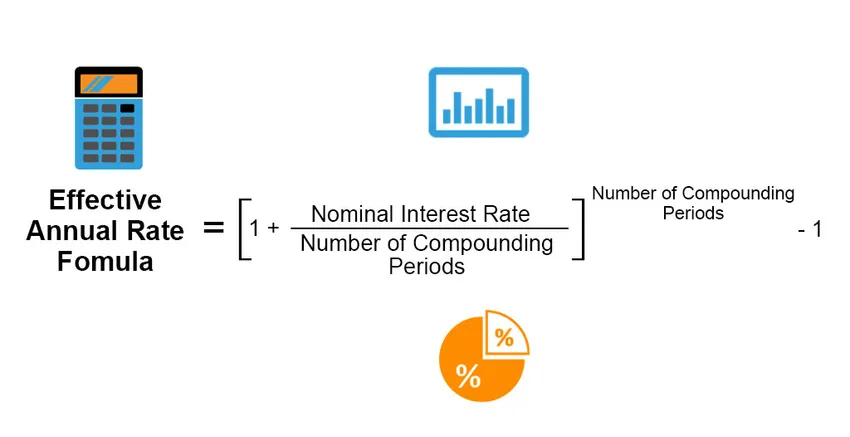
Efektivna godišnja stopa je stvarna kamatna stopa koja se zarađuje ili isplaćuje na investiciji, zajmu ili bilo kojem sličnom financijskom proizvodu, a drugačija je od „nominalne kamatne stope“ zbog razdoblja isplate kamata, složenog od kamatne stope, ukupno vremensko razdoblje zajma ili ulaganja itd. Efektivna godišnja stopa izračunava se sljedećom formulom;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Primjeri učinkovite godišnje formule stopa (sa Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun efektivne godišnje stope.
Ovdje možete preuzeti ovaj obrazac Excel predloška efektivne godišnje stope - Predložak Formule efektivne godišnje stopeFormula efektivne godišnje stope - Primjer br. 1
Pretpostavimo da gospodin X uzima osobni zajam od banke s kamatama od 20%, složene polugodišnje. Izračunajte efektivnu godišnju stopu koristeći podatke.

Riješenje:
Efektivna godišnja stopa izračunava se korištenjem donje formule
Efektivna godišnja stopa = ((1 + (Nominalna kamatna stopa / Broj razdoblja spajanja)) Broj razdoblja složenja) - 1

- Efektivna godišnja stopa = ((1 + (20% / 2)) 2) - 1
- Efektivna godišnja stopa = 21%
Formula efektivne godišnje stope - Primjer br. 2
Pretpostavimo da je gospodin A uložio 100 USD u depozitni certifikat koji isplaćuje nominalnu godišnju kamatnu stopu od 10% koja se tromjesečno sastoji. Izračunajte efektivnu godišnju stopu.

Riješenje:
Efektivna godišnja stopa izračunava se korištenjem donje formule
Efektivna godišnja stopa = ((1 + (Nominalna kamatna stopa / Broj razdoblja spajanja)) Broj razdoblja složenja) - 1
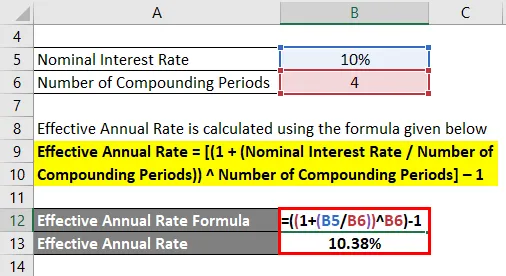
- Efektivna godišnja stopa = ((1 + (10% / 4)) 4) - 1
- Efektivna godišnja stopa = 10, 38%
Formula efektivne godišnje stope - Primjer br. 3
Pretpostavimo da ulaganja u uzajamni fond ostvaruju 15, 50% godišnje kamatne stope kao zarade, dok P2P pozajmljivanje zarađuje 15% godišnje nominalne kamatne stope, složeno mjesečno. Dakle izračunajte efektivnu godišnju stopu za oba slučaja.

Riješenje:
Efektivna godišnja stopa izračunava se korištenjem donje formule
Efektivna godišnja stopa = ((1 + (Nominalna kamatna stopa / Broj razdoblja spajanja)) Broj razdoblja složenja) - 1
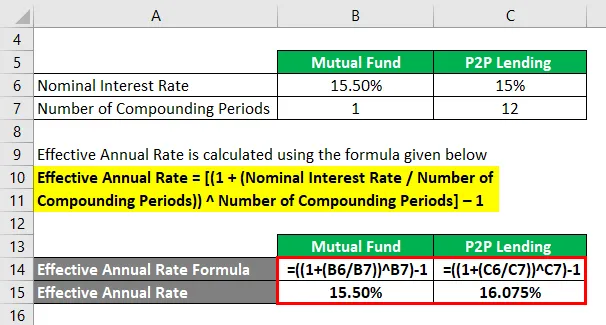
Za uzajamni fond
- Efektivna godišnja stopa = ((1 + (15, 50% / 1)) 1) - 1
- Efektivna godišnja stopa = 15, 50%
Za P2P pozajmljivanje
- Efektivna godišnja stopa = ((1 + (15% / 12)) 12) - 1
- Efektivna godišnja stopa = 16.075%
Obrazloženje
Nominalna kamatna stopa je iskazana stopa na financijski proizvod. U primjeru 3, nominalna stopa prikazana na proizvode čini da uzajamni fond izgleda kao preferirani izbor ulaganja za investitore zbog 0, 50% više godišnje nominalne stope kamate.
Međutim, efektivna godišnja stopa izračunava se uzimajući nominalnu godišnju kamatnu stopu i sastavljajući je za broj određenih razdoblja (12 ako je sjedinjenje mjesečno; 6 ako je sjedinjenje dvomjesečno; 4 ako je tromjesečno; 2 ako je je polugodišnja) primjenjiva u vremenskom rasponu od jedne godine. U slučaju uzajamnog fonda, broj razdoblja sakupljanja godišnje je 1, dok je u slučaju P2P posudbe mjesečno, stoga postoji 12 razdoblja sjedinjenja.
Na temelju formule,
Efektivni godišnji povrat = ((1 + (nominalna kamatna stopa / broj razdoblja sažimanja)) (broj razdoblja složenja)) - 1
Učinkoviti godišnji povrat uzajamnog fonda = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
P2P efektivni godišnji povrat = ((1 + (15, 00% / 12)) 12) - 1 = 16.075%
Relevantnost i upotreba formule efektivne godišnje stope
Formula efektivne godišnje stope koristi se za razlikovanje stvarnog IRR-a (unutarnja stopa povrata) ili godišnjeg prinosa za kamatnu stopu koja se može ili ne mora kombinirati više puta tijekom određenog razdoblja. To bi se moglo vrlo dobro upotrijebiti za usporedbu različitih vrsta mogućnosti ulaganja ili zajamnih kredita uzetih u okviru različitih struktura.
Pretpostavimo da postoje dvije mogućnosti ulaganja, oročeni oročeni depoziti i oročeni depoziti na koje je investitor suzio, uzimajući u obzir njegov / njezin apetit za rizikom i prikladnost. Krajnji je cilj investitora da iz tih depozita izvuče maksimum i ostvari veći povrat. Međutim, oba instrumenta nude malo različite kamatne stope, dok oročeni depozit u Poštama nudi tromjesečno složeni iznos za predmetni termin.
- Iznos ulaganja: Rs 10 lakhs
- Period ulaganja: 5 godina
- Fiksni depozit u banci: 7, 5% godišnje kamate
- Oročeni depozit na poštama: 7, 4% godišnje kamate, složen kvartalno
Po izgledu ponuđenih godišnjih kamatnih stopa, čini se da je banka s fiksnim depozitom bolja opcija. Međutim, ako investitor zaista izračuna tromjesečni složeni faktor oročenog pologa, to rezultira efektivnom godišnjom stopom / povratom od 7, 61%.
Zbog ove male promjene sa 7, 4% na 7, 61% u efektivnoj stopi, investitor bi zaradio ukupno Rs. 4, 42, 848.28 iz ovog određenog instrumenta, dok bi on / ona zaradili Rs. 3, 35, 469.14 iz instrumenta Banke sa fiksnim depozitom.
Ako investitor propusti izračun ove efektivne godišnje stope, izgubio bi priliku da dobije približno više od Rs. 1 lakh od njegove investicije.
Efektivni kalkulator formule godišnje stope
Možete koristiti sljedeći kalkulator efektivne godišnje stope
| Nominalna kamatna stopa | |
| Broj složenih razdoblja | |
| Efektivna godišnja stopa | |
| Efektivna godišnja stopa = | ((1 + (Nominalna kamatna stopa / Broj razdoblja složenja)) Broj razdoblja složenja ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Preporučeni članci
Ovo je vodič za Formulu efektivne godišnje stope. Ovdje smo raspravljali o načinu izračuna efektivne godišnje stope zajedno s praktičnim primjerima. Također nudimo učinkovit godišnji kalkulator stope s besplatnim Excel predložakom. Možete pogledati i sljedeće članke da biste saznali više -
- Kalkulator za formulu realne kamatne stope
- Formula za povrat kapitala zaposlenog | definicija
- Kako izračunati efektivnu kamatnu stopu?
- Koja je sadašnja vrijednost formule anuiteta?