
Uvod u Fibonaccijeve serije u Pythonu
Fibonaccijeva serija u Pythonu, ovo se naziva nizom brojeva, pri čemu je sljedeći broj zbroj sadašnjih dva broja.
Na primjer:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. tako dalje
Dakle, ovdje 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 i tako dalje.
Gledajući gore navedeno, čovjek bi mogao imati određenu predodžbu o onome o čemu govorimo.
Međutim, u smislu matematičkog pravila, može se napisati kao:

Gdje je n-ti broj zbroj broja na mjestima (n-1) i (n-2). Kada je u pitanju implementacija Fibonaccijeve serije, mogao bi se naći određeni broj kodnih jezika putem kojih se to može učiniti.
Međutim, Python je danas široko korišten jezik. Pogledajmo implementaciju Fibonaccijeve serije kroz Python. Treba biti svjestan osnovnih izjava uvjetovanja poput petlje, ako-drugo, dok je petlja, itd. Na Pythonu, prije nego što nastavite ovdje. Ako ne, bilo bi sjajno ako ga netko može revidirati, a zatim zauzeti nadolazeći sadržaj. Ovdje u demo svrhu koristim špijun koji je IDE za programski jezik python-a. Za izvršavanje Python programa možete koristiti bilo koja druga IDE ili Ipython prijenosna računala.
Fibonaccijeva serija u Pythonu
Pogledajmo implementaciju Fibonaccijeva broja i serija uzimajući u obzir prva dva elementa Fibonacije su 0 i 1:
Međutim, možete prilagoditi funkciju Fibonaccija po vašem zahtjevu, ali prvo vidjeti osnove i postupno prijeći na druge.
Python kod za pronalaženje nth Fibonaccijevog broja
Šifra 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Šifra 2:
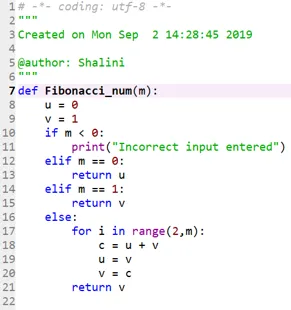
Izlaz:
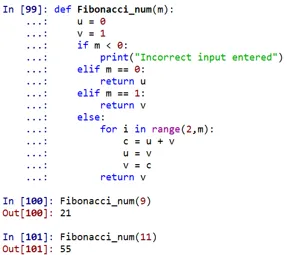
Kao što se može vidjeti, Fibonaccijev broj na 9. mjestu bio bi 21, a na 11. mjestu 55.
- Ovdje je „Weight_num“ definirana funkcija, koja brine za pronalaženje Fibonaccijevog broja uz pomoć određenih uvjeta. Ovu funkciju možete pozvati navođenjem bilo kojeg položaja.
Pogledajmo sada kako se mogu ispisati serije do spomenutog položaja:
Kodirati:
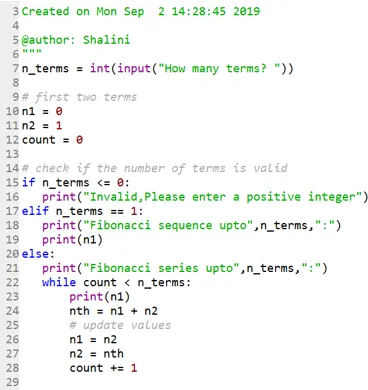
Izlaz:
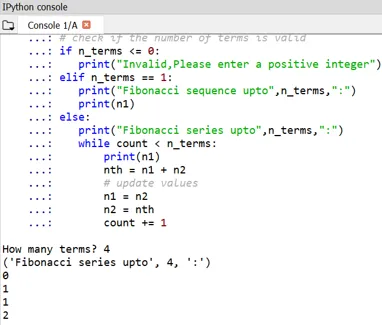
Može se primjetiti da je početak Fibonaccijevih brojeva definiran kao 0 i 1.
- Ako netko želi definirati vlastite početne pojmove, to se može učiniti na isti način ugađanjem n1 i n2. Evo primjera za to:
Recimo sada da želimo da naši početni izrazi budu: n1 = 3, n2 = 5
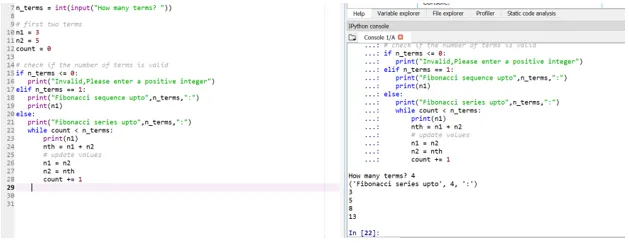
Dakle, ovdje će se odrediti vaš četvrti termin (korisnički unos), ovisno o početnim uvjetima.
Metode pomoću kojih se može generirati Fibonaccijeva serija
Ispod su tri metode pomoću kojih se može stvoriti Fibonaccijeva serija:
1. Kroz generatore
Kodirati:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Izlaz:
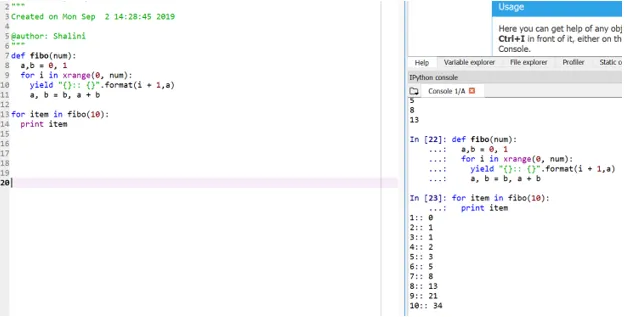
Ova metoda se naziva "generator", jer je funkcija xrange generator brojeva između 0 i broja, a prinos je generator za formatirani izlaz.
Evo što xrange radi za vas:

Ovdje je definiran Fibonaccijev niz u obliku funkcije, unutar koje se za izlaz, brine funkcija petlje, xrange i prinos.
2. Kroz za petlju
Kodirati:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Izlaz:

Kao što se vidi, za ispis Fibonaccijeve serije između 0 i 10. korišten je jednostavan za petlju, a unutar varijable dodijeljene su nove vrijednosti. U i v su zadane početne vrijednosti Fibonaccijeva koje su postavljene na 0 i 1.
Što se tiče kretanja petlje, nova vrijednost u je stara vrijednost v, dok je nova vrijednost v zbroj starih vrijednosti u i v. To se nastavlja do kraja vrijednosti vrijednosti.
3. Kroz rekurziju
Kodirati:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Izlaz:
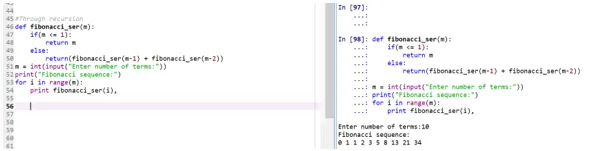
- Funkcija „Meridian_server“ poziva na sebe da ispisuje Fibonaccijevu seriju.
- I otuda je metoda dobila naziv "rekurzija".
Slijede koraci:
- Ovdje se od korisnika traži da unese mjesto do kojeg treba ispisati Fibonaccijeve serije.
- Brojka prolazi kroz funkciju "Weight_ser".
- Uvjet se provjerava, ako je navedena duljina manja od 1 ili nije. Ako je odgovor da, rezultat se daje odmah.
- Međutim, ako je duljina veća od 1, rekurzivni pozivi upućuju se na "vredan_ser" s argumentima čija je duljina manja od 1 i 2, tj. Vrednosni_ser (m-1) i napon_ser (m-2).
- Dakle, rekurzija daje željeni izlaz i ispisuje ga.
- Dakle, ukratko, Raspravljali smo o tri načina za prikazivanje Fibonaccijeve serije.
- Kroz petlju, generatore i rekurziju.
Sva tri Python koda sažeta su
Ispod su tri python koda:
1. Kroz generatore
Kodirati:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Kroz za petlju
Kodirati:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Kroz rekurziju
Kodirati:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Sažeto gore su svi postupci, treba vježbati da bi se svi dobro uhvatili.
Izlaz:
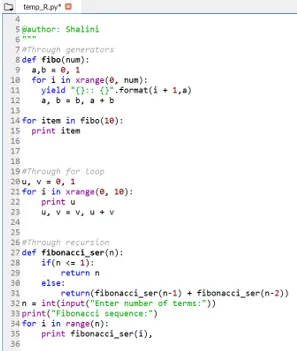
Zaključak
Kroz gornji sadržaj Fibonaccija moglo bi se dobiti kristalno jasno razumijevanje Fibonaccijevih brojeva i serija, specijaliziranih za piton. Jednom, netko će se složiti s logikom Fibonaccijeve serije, generiranje drugog skupa serija, rad s drugim brojevima i raznim metodama sada će biti pravi potez za vas. Logički pristup je jedini način da se to istakne.
Preporučeni članci
Ovo je vodič za Fibonaccijeve serije u Pythonu. Ovdje razgovaramo o Fibonaccijevim brojevima i serijama, specijaliziranim za pyton, generiranje drugog skupa serija, rad s drugim brojevima i raznim metodama. Možete i pregledati naše druge povezane članke da biste saznali više -
- Generator slučajnih brojeva u Pythonu
- Matematičke funkcije u Pythonu
- Čimbenik u Pythonu
- Inkapsulacija u Pythonu
- Serija Fibonaccije na Javi
- Značajke Pythona
- Faktorski program u JavaScript-u
- Generator slučajnih brojeva u Matlabu
- Generator slučajnih brojeva u C #
- Inkapsulacija u JavaScriptu