
Koeficijent formule varijacije (Sadržaj)
- Formula
- Primjeri
Koliki je koeficijent formule varijacije?
U statistici, koeficijent varijacije koji se također naziva CV je alat koji nam pomaže da odredimo kako se podatkovne točke u skupu podataka raspoređuju oko srednje vrijednosti. U osnovi, prvo se crtaju sve podatkovne točke, a zatim se koristi koeficijent varijacije za mjerenje disperzije tih točaka jedna od druge i srednje vrijednosti. Tako nam pomaže u razumijevanju podataka i uvida u obrazac koji tvori. Izračunava se kao omjer standardnog odstupanja skupa podataka prema srednjoj vrijednosti. Veći koeficijent varijacije znači da je veća razina disperzije podataka oko srednje vrijednosti. Slično tome, manja je vrijednost koeficijenta varijacije, manja je disperzija i precizniji će biti rezultati. Čak i ako se prosjek dviju podataka značajno razlikuje, koeficijent varijacije vrlo je koristan za usporedbu stupnja varijacije iz jedne serije podataka u drugu.
Formula za koeficijent varijacije dana je:
Coefficient of Variation = Standard Deviation / Mean
Koraci za izračunavanje koeficijenta varijacije:
Korak 1: Izračunajte sredinu skupa podataka. Srednja vrijednost je prosjek svih vrijednosti i može se izračunati tako da se uzme zbroj svih vrijednosti i zatim dijeli s brojem podataka.
Korak 2: Zatim izračunajte standardno odstupanje skupa podataka. To je malo zahtjevan proces. Odstupanje norme može se izračunati kao: √ (Σ (X i - X m ) 2 / (n - 1)) . X i je prva točka podataka, a X m je sredina skupa podataka. Alternativno, možemo pronaći standardno odstupanje u excelu pomoću funkcije STDEV.S ().
Korak 3: Podijelite standardno odstupanje s prosjekom da biste dobili koeficijent varijacije.
Primjeri koeficijenta formule varijacije (s Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun koeficijenta varijacije.
Ovaj koeficijent predloška formule varijacije Formule možete preuzeti ovdje - Koeficijent predloška formule varijacije varijacijeKoeficijent formule varijacije - Primjer br. 1
Recimo da imamo dva skupa podataka A&B i svaki sadrži 20 slučajnih podataka. Izračunajte koeficijent varijacije za skup podataka X&Y.
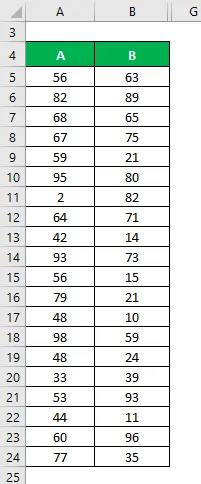
Riješenje:
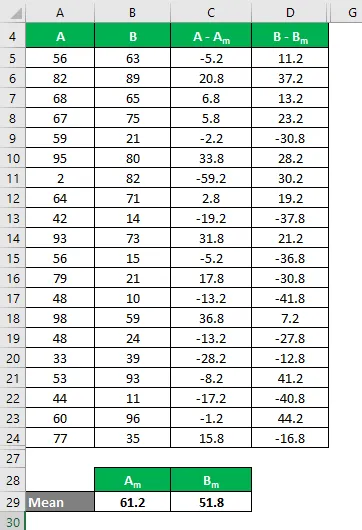
Srednja vrijednost izračunava se kao:
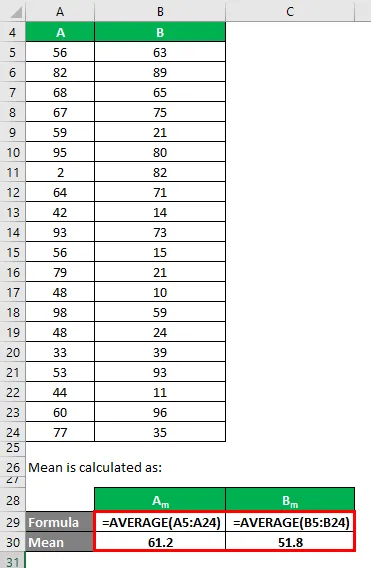
- Srednja vrijednost skupa podataka A = 61.2
- Srednja vrijednost skupa podataka B = 51.8
Sada moramo izračunati razliku između podatkovnih točaka i srednje vrijednosti.
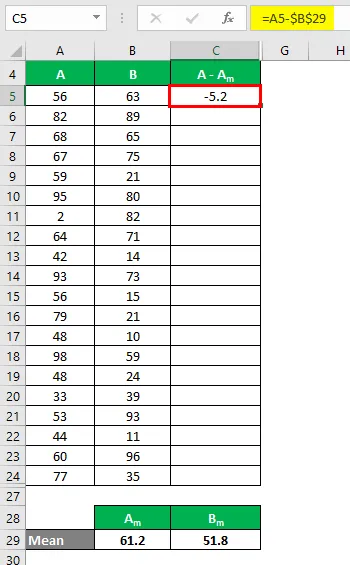
Slično tome, izračunajte za sve vrijednosti skupa podataka A.
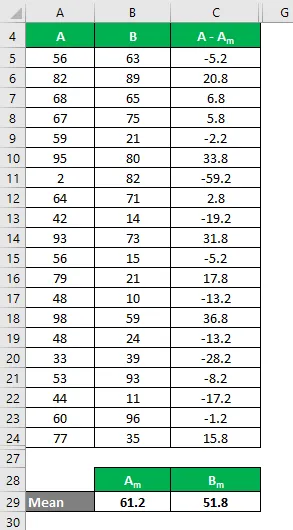
Slično tome, izračunajte za sve vrijednosti skupa podataka B.
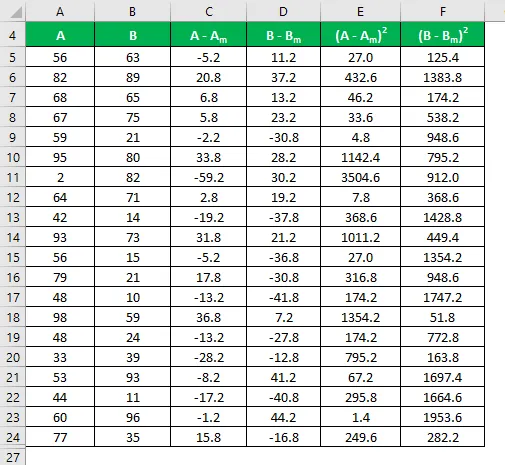
Izračunajte kvadrat razlike za oba skupa podataka A i B.
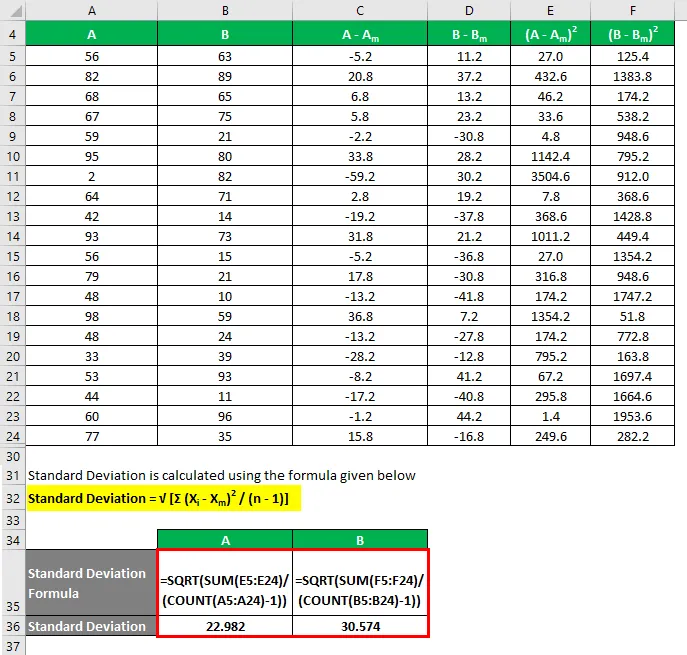
Standardno odstupanje izračunava se prema nižoj formuli
Standardno odstupanje = √ (Σ (X i - X m ) 2 / (n - 1))
Koeficijent varijacije se izračunava dolje navedenom formulom
Koeficijent varijacije = standardno odstupanje / srednje vrijednosti
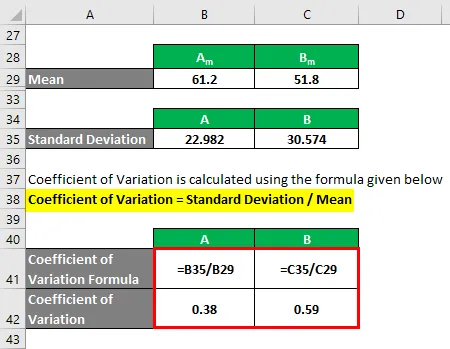
- Koeficijent varijacije A = 22, 982 / 61, 2 = 0, 38
- Koeficijent varijacije B = 30, 574 / 51, 8 = 0, 59
Ako ovdje vidite, B ima veći koeficijent varijacije od A, što znači da su podatkovne točke B višestruko raspodijeljene od A.
Koeficijent formule varijacije - Primjer br. 2
Recimo da ste ulagač vrlo rizičan i želite uložiti novac u burzu. Budući da je apetit za rizikom nizak, želite uložiti u sigurne zalihe s nižim standardnim odstupanjem i koeficijentom varijacije. Ušli ste u uži izbor 3 dionice na temelju njihovih temeljnih i tehničkih podataka i želite odabrati 2 dionice. Prikupljali ste i podatke o njihovim povijesnim povratima u posljednjih 15 godina.
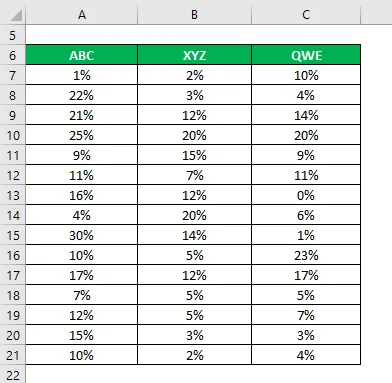
Riješenje:
Srednja vrijednost izračunava se kao:
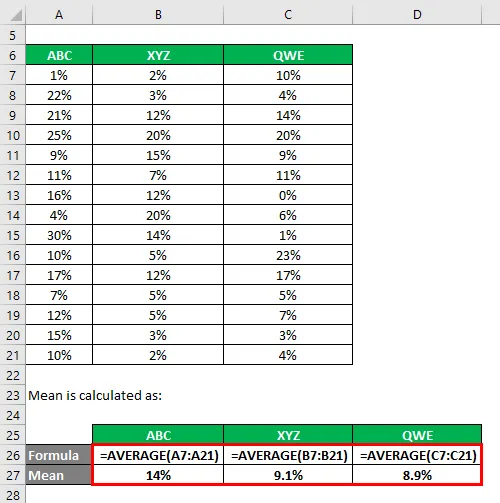
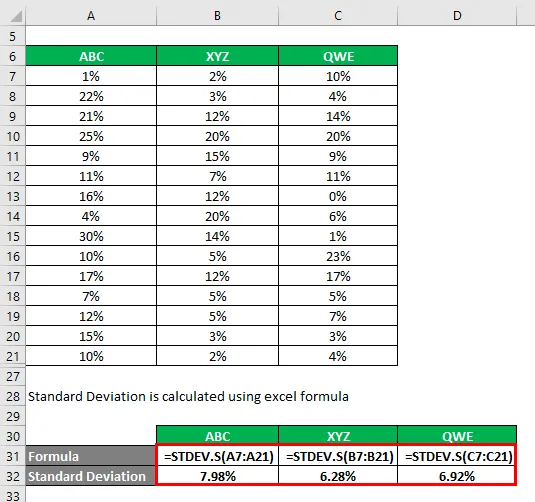
Standardno odstupanje izračunava se pomoću excelove formule
Koeficijent varijacije se izračunava dolje navedenom formulom
Koeficijent varijacije = standardno odstupanje / srednje vrijednosti
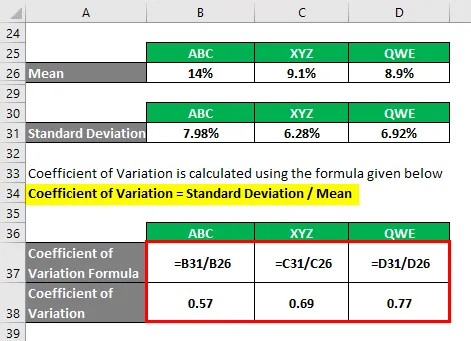
- Koeficijent varijacije ABC = 7, 98% / 14% = 0, 57
- Koeficijent varijacije XYZ = 6, 28% / 9, 1% = 0, 69
- Koeficijent varijacije QWE = 6, 92% / 8, 9% = 0, 77
Na temelju podataka, izabrati ćete dionice ABC i XYZ za ulaganje jer imaju najmanji koeficijent varijacije.
Obrazloženje
Budući da je koeficijent varijacije mjera rizika, pomaže u mjerenju volatilnosti cijena dionica i drugih financijskih instrumenata. Također pomaže ulagačima i analitičarima da uspoređuju rizike povezane s različitim potencijalnim ulaganjima.
Koeficijent varijacije sličan je standardnom odstupanju, ali se standardno odstupanje dviju varijabli ne može usporediti s korisnim. Ali pomoću standardne devijacije i srednje vrijednosti relativna usporedba postaje smislenija. Postoji i ograničenje koeficijenta varijacije. Pretpostavimo da je sredina skupa podataka jednaka nuli. U tom će slučaju ovaj alat postati neučinkovit. I ne samo to, ako imamo skup podataka koji ima mnogo pozitivnih i negativnih vrijednosti, koeficijent varijacije postaje vrlo problematičan. Stoga je korisnije samo ako su skupovi podataka s istim znakom plus-minus.
Relevantnost i upotreba koeficijenta formule varijacije
Koeficijent varijacije ima relevantnost u mnogim drugim područjima osim statistike. Primjerice, u području financija koeficijent varijacije je mjera rizika. Slično je standardnom odstupanju jer se koristi i kao mjera rizika, ali razlika je u tome što je koeficijent varijacije bolji pokazatelj relativnog rizika. Na primjer, recimo očekivani povrat A od 15% i B očekivani povrat od 10%, a A standardno odstupanje od 10%, dok B ima standardno odstupanje od 5%. Za odabir boljeg ulaganja može se koristiti koeficijent varijacije. Koeficijent varijacije A je 10/15 = 0, 666, a koeficijent varijacije B je 5/10 = 0, 5. Dakle, B je bolja investicija od A.
Preporučeni članci
Ovo je vodič za Koeficijent formule varijacije. Ovdje smo raspravljali o tome kako izračunati koeficijent varijacije pomoću formule zajedno s praktičnim primjerima i download-om Excel predloška. Možete pogledati i sljedeće članke da biste saznali više -
- Što je prilagođena R kvadratna formula?
- Primjeri koeficijenta formule određivanja
- Kako izračunati koeficijent korelacije pomoću formule?
- Formula kovarijancije s predloškom Excela