
Interpolacijska formula (Sadržaj)
- Formula
- Primjeri
Što je interpolacijska formula?
Izraz "Interpolacija" odnosi se na tehniku dogradnje krivulje koja se koristi u predviđanju intermedijarnih vrijednosti i obrazaca na temelju dostupnih povijesnih podataka zajedno s nedavnim podacima. Drugim riječima, tehnika interpolacije može se upotrijebiti za predviđanje nedostajućih podatkovnih točaka između raspoloživih točaka podataka.
Formula za interpolaciju u osnovi gradi funkciju za nepoznatu varijablu (y) na temelju neovisne varijable i najmanje dvije podatkovne točke - (x 1, y 1 ) i (x 2, y 2 ). Matematički se predstavlja kao
Formula,
y = (y 2 – y 1 ) / (x 2 – x 1 ) * (x – x 1 ) + y 1
gdje,
- x = nezavisna varijabla
- x 1 = 1. neovisna varijabla
- x 2 = 2. nezavisna varijabla
- y 1 = Vrijednost funkcije pri vrijednosti X 1
- y 2 = Vrijednost funkcije pri vrijednosti x 2
Primjer interpolacijske formule (s Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun interpolacijske formule.
Ovdje možete preuzeti ovaj Interpolation Formula Excel predložak - Interpolation Formula Excel predložakInterpolacijska formula - Primjer # 1
Uzmimo za primjer vrućeg štapa da ilustriramo pojam interpolacije. Pretpostavimo da je temperatura štapa bila u 9:30 ujutro 100 ° C što se postupno spuštalo na 35 ° C u 10, 00 sati Na osnovu datih podataka pronađite temperaturu štapa u 9.40 sati.
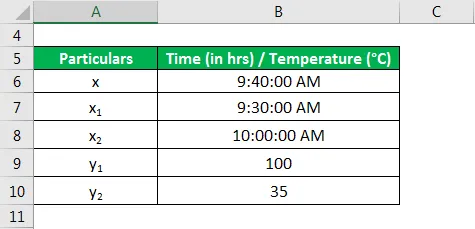
Riješenje:
Temperatura štapa (y) izračunava se prema nižoj formuli.
y = (y 2 - y 1 ) / (x 2 - x 1 ) * (x - x 1 ) + y 1
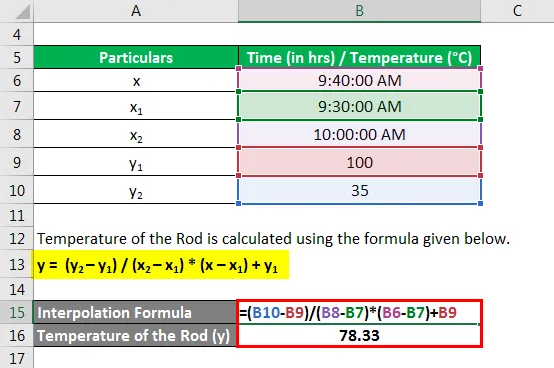
- Temperatura šipke (y) = (35 - 100) / (1000 - 930) * (940 - 930) + 100 ֯ C
- Temperatura štapa (y) = 78, 33 ֯ C
Stoga je temperatura štapa bila 78, 33 ° C u 9, 40 ujutro
Interpolacijska formula - Primjer br. 2
Uzmimo za znatiželjni slučaj Johna Doea koji je u posljednjih nekoliko mjeseci dobio značajnu težinu. Kao takav, njegov je liječnik odlučio nadzirati njegovu težinu i tako je počeo pratiti njegovu težinu svakih 6 dana tijekom posljednjih 60 dana. Prikupljene su sljedeće informacije:
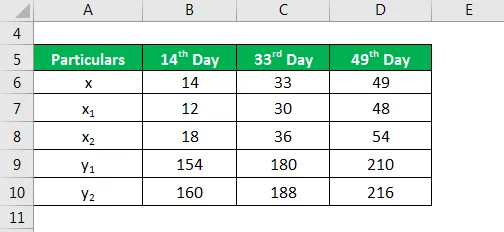
Riješenje:
Masa Johna izračunava se dolje opisanom formulom.
y = (y 2 - y 1 ) / (x 2 - x 1 ) * (x - x 1 ) + y 1
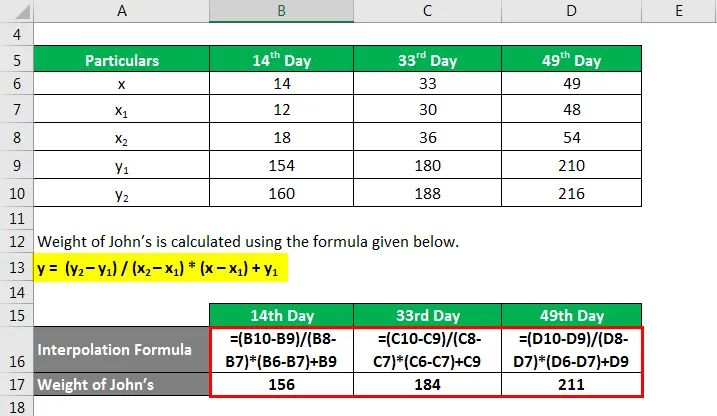
14. dana
- 14. dana = (160 - 154) / (18 - 12) * (14 - 12) + 154
- 14. dana = 156 lbs
33. dan
- 33. dan = (188 - 180) / (36 - 30) * (33 - 30) + 180
- 33. dan = 184 lbs
49. dana
- 49. dana = (216 - 210) / (54 - 48) * (49 - 48) + 210
- 49. dana = 211 lbs
Stoga je Ivanova težina 14., 33. i 49. dana bila 156 lbs, 184 lbs, odnosno 211 lbs.
Obrazloženje
Formula za interpolaciju može se izračunati pomoću sljedećih koraka:
Korak 1: Prvo, identificirajte neovisne i ovisne varijable za funkciju.
Korak 2: Zatim prikupite što više povijesnih i trenutačnih podataka kako biste izgradili funkciju. Provjerite postoje li najmanje dvije podatkovne točke jer su to minimalne potrebne podatkovne točke.
Korak 3: Zatim izračunajte nagib raspoloživih podatkovnih točaka tako što ćete razliku između ordinata podijeliti s apscisom raspoloživih podataka.
Nagib = (y 2 - y 1 ) / (x 2 - x 1 )
Korak 4: Konačno, funkcija za interpolaciju može se izvesti množenjem nagiba (korak 3) s razlikom između neovisne varijable i apscide bilo koje podatkovne točke, a zatim dodavanju odgovarajuće ordinate u rezultat kao što je prikazano u nastavku.
y = (y 2 - y 1 ) / (x 2 - x 1 ) * (x - x 1 ) + y 1
Relevantnost i upotreba interpolacijske formule
Važnost tehnike interpolacije može se shvatiti iz činjenice da su linearne interpolaciju, kako se vjeruje, koristili babilonski matematičari i astronomi u posljednja tri stoljeća prije Krista, dok su je Grci i Hipparh koristili u 2. stoljeću prije Krista. Jedna od osnovnih varijanti interpolacije je tehnika linearne interpolacije koju analitičari najčešće koriste u području matematike, financija i računalnog programiranja. Imajte na umu da je interpolacija statistički i matematički alat koji se koristi za predviđanje intermedijarnih vrijednosti između dviju točaka.
Preporučeni članci
Ovo je vodič za Interpolacijsku formulu. Ovdje ćemo raspraviti kako izračunati interpolacijsku formulu zajedno s praktičnim primjerima. Također pružamo i predloženi excel predložak za preuzimanje. Možete pogledati i sljedeće članke da biste saznali više -
- Formula neto novčanog toka
- Podržana beta formula
- Pomična prosječna formula
- Povrat prodajne formule