
Uvod u standardne primjere odstupanja
Dosta je primjera standardnih odstupanja. Standardno odstupanje je mjera raširenosti skupa podataka, tj. Kako su raspoređeni brojevi. Korisno je za usporedbu različitih skupova podataka koji mogu imati istu sredinu, ali različit raspon. Sljedeći različiti primjer standardnog odstupanja daje razumijevanje o najčešćim vrstama situacija u kojima se izračunava standardno odstupanje i kako se može izračunati isto
Primjeri standardnog odstupanja
Ispod su primjeri Standard Devijata
Standardno odstupanje - Primjer br. 1
Dionice Tvrtke Z prodaju za 50 USD po dionici i iste ponude sljedeće isplate za sljedeću godinu:
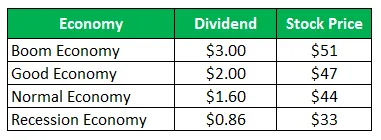
Izračunajte standardno odstupanje kada su sva četiri scenarija dana podjednako vjerojatna.
Riješenje:
Izračuni povrata perioda zadržavanja (HPR) su sljedeći -
Formula HPR-a
HPR = ((vrijednost kraja razdoblja - izvorna vrijednost) + prihod) / izvorna vrijednost) * 100
Za ekonomiju buma
- HPR (Boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (dobro) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normalno) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recesija) = ((33-50) + 0, 86) / 50 = -32, 28%
Proračun očekivanog povrata
Kako su svi scenariji podjednako vjerojatni, vjerojatnost svih će biti ¼
Formula očekivanog povratka
Očekivani povratak = (vjerojatnost procvata * povratak iz procvata) + (vjerojatnost dobra * povratak iz dobra) + (vjerojatnost normalnog * povratak iz normalnog) + (vjerojatnost recesije * povratak iz recesije)
- Očekivani povrat = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Očekivani povrat = -8, 77%
Proračun standardnog odstupanja
Formula varijance
Varijanca = (vjerojatnost buma * (povratak iz strele - ukupni očekivani povratak) 2) + (vjerojatnost dobra * (povratak iz dobra - ukupan očekivani povratak) 2) + (vjerojatnost normalnog * (povratak iz normalnog - ukupan očekivani povratak)) 2 ) + (vjerojatnost recesije * (povratak iz recesije - ukupno očekivani povratak) 2)
- Varijacija = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8.77)) 2
- Varijanca = 219, 95
Formula standardnog odstupanja
Standardno odstupanje bit će kvadratni korijen varijance
Standardno odstupanje = √ Varijanta
- Standardno odstupanje = √ 219, 95
- Standardno odstupanje = 14, 83%
Primjer standardnog odstupanja - 2
Standardna devijacija u slučaju dviju tvrtki u portfelju
Uobičajena dionica Tvrtke A prodaje se za 28 dolara po dionici i iste ponude nakon isplate za sljedeću godinu

Uobičajena dionica tvrtke B prodaje se za 93 dolara po dionici, a iste ponude nude sljedeće otplate za sljedeću godinu:

(a) Izračunajte standardni odstupanje tvrtke A
(b) Izračunajte standardno odstupanje tvrtke B
(c) Izračunajte standardno odstupanje portfelja ako je polovina ulaganja izvršena u kompaniji A, a polovina u kompaniji B
Riješenje:
Za tvrtku A
Izračuni povrata perioda zadržavanja (HPR)
Formula HPR-a
HPR = ((vrijednost kraja razdoblja - izvorna vrijednost) + prihod) / izvorna vrijednost) * 100
- HPR (bum) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normalno) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recesija) = ((38-28) + 5) / 28 = 53, 57%
Proračun očekivanog povrata poduzeća A
Formula očekivanog povratka
Očekivani povratak = (vjerojatnost buma * povratak iz strele) + (vjerojatnost normalnog * povratak iz normalnog) + (vjerojatnost recesije * povratak iz recesije)
- Očekivani povrat = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Očekivani povrat = 3, 84%
Proračun tvrtke Standard Deviation A
Formula varijance
Varijanca = (Vjerojatnost buma * (Povratak iz strele - Ukupni očekivani povratak) 2) + (Vjerovatnoća normalnog * (Povratak iz normalnog - Ukupni očekivani povratak) 2 ) + (Vjerojatnost recesije * (Povratak iz recesije - Ukupni očekivani povratak) 2)
- Varijanca = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varijanca = 895, 15
Formula standardnog odstupanja
Standardno odstupanje bit će kvadratni korijen varijance
Standardno odstupanje = √ Varijanta
- Standardno odstupanje = √ 895, 15
- Standardno odstupanje = 29, 92%
Za tvrtku B
Izračuni povrata perioda zadržavanja (HPR)
Formula HPR-a
HPR = ((vrijednost kraja razdoblja - izvorna vrijednost) + prihod) / izvorna vrijednost) * 100
HPR (bum) = ((200-93) +7) / 93 = 122, 58%
HPR (normalno) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (recesija) = ((4-93) +2) / 93 = -93, 55%
Proračun očekivanog povrata
Formula očekivanog povratka
Očekivani povratak = (vjerojatnost buma * povratak iz strele) + (vjerojatnost normalnog * povratak iz normalnog) + (vjerojatnost recesije * povratak iz recesije)
- Očekivani povrat = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Očekivani povrat = 43, 04%
Proračun standardnog odstupanja
Formula varijance
Varijanca = (Vjerojatnost buma * (Povratak iz strele - Ukupni očekivani povratak) 2) + (Vjerovatnoća normalnog * (Povratak iz normalnog - Ukupni očekivani povratak) 2 ) + (Vjerojatnost recesije * (Povratak iz recesije - Ukupni očekivani povratak) 2)
- Varijanca = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varijanca = 6783, 65
Formula standardnog odstupanja
Standardno odstupanje bit će kvadratni korijen varijance
Standardno odstupanje = √ Varijanta
- Standardno odstupanje = √6783, 65
- Standardno odstupanje = 82, 36%
Izračun očekivanog povrata i standardnog odstupanja polovine portfelja uloženog u poduzeće A i polovine u kompaniju B.
Standardno odstupanje od tvrtke A = 29, 92%
Standardno odstupanje od tvrtke B = 82, 36%
Težina tvrtke A = 0, 50
Težina tvrtke B = 0, 50
Formula standardnog odstupanja portfelja
Standardno odstupanje portfelja = (Težina tvrtke A * Očekivani povrat tvrtke A) + ((Težina tvrtke B * Očekivani povrat tvrtke B)
- Standardno odstupanje portfelja = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standardno odstupanje portfelja = 56, 14%
Analiza
Standardno odstupanje portfelja je niže nego kod pojedinačnih dionica jer su zalihe raznolike u različitim dionicama. Diverzifikacija dovodi do smanjenja rizika ukoliko ne postoji savršena korelacija između povrata portfeljskih ulaganja.
Zaključak - Standardni primjeri odstupanja
Standardno odstupanje mjeri raširenost skupa podataka koja je relativna po srednjoj vrijednosti. Izračunava se kao kvadratni korijen varijance. Što je veće standardno odstupanje vrijednosnog papira, veće će biti odstupanje između svake cijene i prosjeka, što pokazuje da je raspon cijena velik. Gore navedeni primjeri neki su od primjera Standardnog odstupanja na različite načine. Postoje i razni drugi primjeri koji pokazuju da se standardno odstupanje može izračunati pomoću drugih podataka.
Preporučeni članci
Ovo je vodič za standardne primjere odstupanja. Ovdje ćemo raspraviti različite primjere standardnog odstupanja zajedno s detaljnim objašnjenjem . Možete također pogledati sljedeće članke da biste saznali više -
- Primjer fiksnih troškova
- Primjer varijabilnog troška
- Kvantitativni primjer istraživanja
- Primjeri monopolističke konkurencije