Primjer složenog kamata - Praktični primjeri s formulom

Uvod u primjer složenog kamata

Mnogo je primjera složenih interesa. Sljedeći različiti primjeri složenih kamata daju razumijevanje najčešće vrste situacija u kojima se složeni kamata izračunava i kako se može izračunati isto. Budući da postoji više područja i situacija u kojima se složeni kamati mogu izračunati, nije moguće navesti sve vrste primjera. Dakle, u nastavku su navedeni neki od primjera složenih interesa koji prikazuju različite situacije

Primjeri složenog interesa (s Excelovim predloškom)

Uzmimo primjer kako bismo bolje razumjeli izračun Složene kamate.

Ovdje možete preuzeti ovaj primjer složenog kamata Excel predložak - Primjer složenog kamata Predložak Excela Ispod su primjeri složenog interesa:

Primjer složenog kamata -1

Harry želi uštedu započeti od novca koji je zaradio. Zatim odlučuje položiti početni iznos od 10.000 USD na štedni račun s visokim kamatama. Kamatna stopa u ovom slučaju bit će 15% godišnje složena. Trenutno je dob harryja 40 godina, a mirovinu planira povući u dobi od 60 godina. To znači da Harry ima vremensko razdoblje od 40 godina da može akumulirati kamatu. Izračunajte iznos novca koji će Harry dobiti u dobi od 60 godina. Također, pripremite tablicu za prikaz godišnjih kamata i vrijednosti računa.

S obzirom,

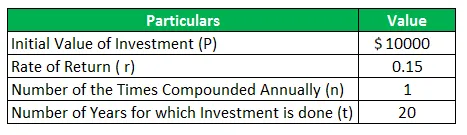
Riješenje:

Koristeći dane informacije, izračunava se složena kamata i iznos koji treba primiti u dobi od 60 godina kako slijedi:

Izračun buduće vrijednosti ulaganja pomoću formule složenih kamata je kako slijedi:

A = P (1 + r / n) ^nt

A = 10 000 USD (1 + 0, 15 / 1) ^{1 * 20}
A = 10 000 USD (1 + 0, 15) ²⁰
A = 10 000 USD (1, 15) ²⁰
A = 10 000 USD * 16, 367
A = 163, 665, 37 USD

Tablica za prikaz godišnjih kamata i vrijednosti računa

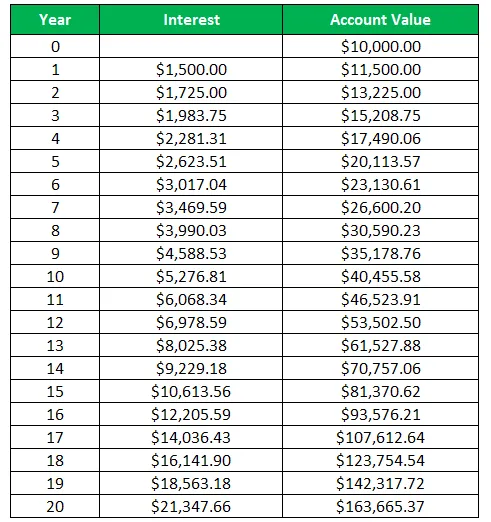
Ovdje se kamata izračunava kao:

Kamata = Početni iznos investicije * Kamatna stopa (r)
Kamata = 10000 * 15%
Kamata = 1500 USD

Slično je i za sve godine.

a vrijednost računa izračunava se kao:

Vrijednost računa = Početni iznos ulaganja + kamata
Vrijednost računa = 10000 + 1500
Vrijednost računa = 11500 USD

Slično je i za sve godine.

U ovom primjeru možemo vidjeti da vrijednost investicije koja je u početku napravljena u iznosu od 10 000 USD postaje 163 665, 37 USD na kraju razdoblja od 20 godina. Ovo naglašava snagu složenja, jer uz pomoć složenih kamata svoje novce množimo u više navrata bez aktivnog upravljanja investicijom. Ovdje je Harry mogao zaraditi na ranije zarađenim kamatama.

Primjer složenog kamata -2

Sam ulaže u početno ulaganje od 10 000 USD za razdoblje od 5 godina. Želi znati iznos ulaganja koji će dobiti nakon pet godina ako investicija zaradi povrat od 6% godišnje složen.

S obzirom,

Koristeći dane informacije, izračunava se složena kamata i iznos koji treba primiti nakon razdoblja od 5 godina kako slijedi:

Riješenje:

Izračun buduće vrijednosti investicije pomoću formule složenih kamata je kako slijedi:

A = P (1 + r / n) ^nt

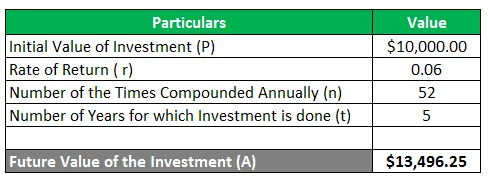
A = 10 000 USD (1 + 0, 6 / 52) ^{52 * 5}

A = 10 000 USD (1 + 0, 00115) ²⁶⁰

A = 10 000 USD (1.00115) ²⁶⁰

A = 10.000 USD * 1.3496

A = 13 496, 25 USD

U ovom primjeru možemo vidjeti da vrijednost investicije koja je u početku napravljena u iznosu od 10 000 USD postaje 13 496, 25 USD na kraju petogodišnjeg razdoblja kada se sastavljanje vrši na tjednoj osnovi. Složenost povećava vrijednost ulaganja na kraju razdoblja jer se kamata zarađuje i na ranije zarađenim kamatama. Ovdje se složenje radi 52 puta jer postoji 52 tjedna u godini.

Zaključak - Primjer složenog kamata

Složena kamata daje više kamata u odnosu na jednostavne kamate, jer se dobiva naplatom kamate na preostalu glavnicu, uključujući kamate za razliku od jednostavnih kamata, gdje se kamata obračunava na prvobitni iznos glavnice i ne obračunava se kamata nad kamatama. Moć sakupljanja pomaže u rastu ulaganja s većom brzinom koja ima obilježja eksponencijalne funkcije. Rezultat je činjenice da se unatoč isplativanju ulaganja reinvestiraju kako bi brže rasli. To se vrlo često koristi u uobičajenim poslovnim praksama, bilo da je riječ o zajmu ili depozitu. Štoviše, koliko često se sastavljanje vrši, također će biti odlučujući faktor rasta. Pretpostavimo da ako je u bilo kojoj određenoj frekvenciji miješanja mjesečno, tada će njena godišnja stopa biti veća od frekvencije miješanja polugodišnje ili godišnje.

Preporučeni članci

Ovo je vodič za Primjer složenog interesa. Ovdje smo raspravljali kako izračunati složene kamate koristeći svoju formulu zajedno s praktičnim primjerima. Možete također pogledati sljedeće članke da biste saznali više -