
Sastavljena formula godišnje stope rasta (Sadržaj)
- Formula
- Primjeri
- Kalkulator
Koja je sastavljena formula godišnjeg rasta?
Sklapanje je učinak kada investicija zarađuje ne samo na glavnoj komponenti, već i daje kamate. Tako složena godišnja stopa rasta je efektivni godišnji rast zarade od ulaganja s obzirom na sjedinjenje u sliku. To u osnovi pretpostavlja da se kamata zarađena svake godine reinvestira i da zarađuje jednaku kamatu kao i iznos glavnice. To je razlog što je složena godišnja stopa rasta uvijek viša od jednostavne kamatne stope. Mnoga ulaganja poput uzajamnih fondova, prinosa na burzi nisu baš linearna i na vrlo nestabilan način.
Sastavljena godišnja stopa rasta pomaže u izravnavanju tog povrata i reći će koliko je investitor zaradio tijekom trajanja ulaganja s obzirom na činjenicu da se sva zarada u tom razdoblju reinvestira istom stopom. Zbog ovog efekta izravnavanja pomaže nam u usporedbi skupova podataka s različitom razinom volatilnosti. Vrlo se često koristi u svrhu financijske analize.
Završni iznos investicije = Početni iznos (1 + CAGR) Broj godina
Formula za složenu godišnju stopu rasta -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Ova formula je primjenjiva ako se ulaganje gomila godišnje, znači da novac ponovo ulažemo na godišnjoj osnovi. Ali ponekad se desi da želimo izračunati stopu do koje se dolazi do tromjesečja, mjesečno i dnevno. Pa za to koristimo donju formulu:
Završni iznos investicije = Početni iznos (1 + CAGR / sastavna frekvencija) (broj godina * složena frekvencija)
Dakle, formula za složenu godišnju stopu rasta -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Učestalost složenica:
- Polugodišnje sažimanje: 2
- Tromjesečno složeni: 4
- Mjesečna učestalost: 12 i tako dalje
Primjeri CAGR formule (s Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun CAGR formule.
Ovdje možete preuzeti ovaj složeni Excel obrazac za godišnju stopu rasta ovdje - Složeni predložak Excela za godišnju stopu rasta.CAGR formula - Primjer # 1
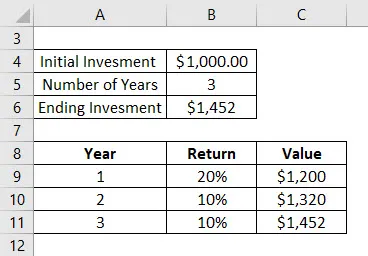
Recimo da ste uložili 1000 USD u uzajamne fondove prije 3 godine. Slijedi povratak koji ste dobili za ove 3 godine:
- Prve godine dobili ste 20% povećanje vrijednosti. Dakle, ukupna vrijednost je 1200 dolara na kraju 1. godine
- U drugoj godini, dobili ste 10% povećanje vrijednosti. Dakle ukupna vrijednost je 1320 dolara na kraju 2. godine
- Treću godinu, dobili ste 10% povećanje vrijednosti. Dakle, ukupna vrijednost je 1452 USD na kraju 3. treće godine
CAGR se izračunava dolje navedenom formulom
CAGR = (Završni iznos investicije / Početni iznos) (1 / Broj godina) - 1
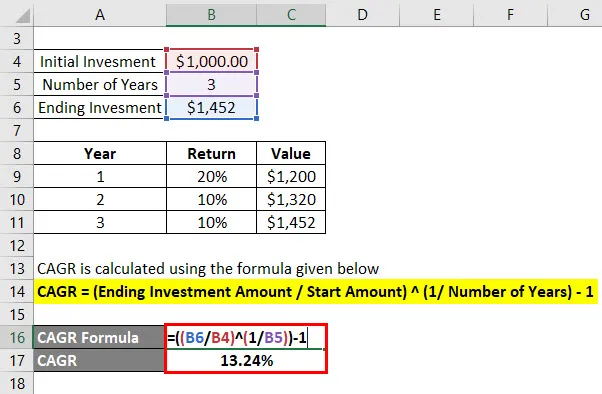
- CAGR = (1.452 USD / 1.000 $) (1/3) - 1
- CAGR = 13, 24%
Ovdje možemo vidjeti kako godišnji prinos za sve tri godine je različit i varira, ali složena godišnja stopa rasta daje nam jedinstvenu stopu koju možemo usporediti s različitim mogućnostima ulaganja.
CAGR formula - Primjer # 2
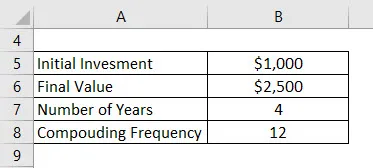
Recimo da ste uložili 1000 dolara u banku, a novac želite zadržati u banci 4 godine. Recimo sada da ukupni iznos koji dobijete nakon 4 godine iznosi 2500 USD. Banka nudi stopu s mjesečnim sabiranjem. Izračunajte CAGR.
CAGR se izračunava dolje navedenom formulom
CAGR = sastavna učestalost * ((završni iznos ulaganja / početni iznos) (1 / (broj godina * složena učestalost)) - 1)
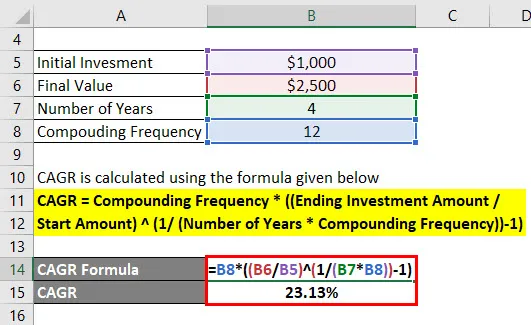
- CAGR = 12 * ((2.500 USD / 1.000 $) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Tako složena godišnja stopa rasta iznosi 23, 13%.
Objašnjenje sastavljene formule godišnje stope rasta
Iako je složena godišnja stopa rasta godišnja stopa ulaganja, to je samo teoretski podatak i nije pravi prinos. Glavna pretpostavka ovdje je što se sva zarada reinvestira po istoj stopi za razdoblje ulaganja, ali stopa neće ostati za sve godine i ne možemo uložiti svoj novac po istoj stopi. Dakle, to je jedini reprezentativni postotak koji nam govori da bismo mogli završiti ako se sav novac reinvestira na kraju svake godine po toj stopi. Dakle, postoje neke ključne točke koje bismo trebali uzeti u obzir pri korištenju složene godišnje stope rasta.
Također, bit ćemo stvarno oprezni o ulaganju koje traje dugo. Na primjer, ako je razdoblje ulaganja vrlo dugo, recimo 20 godina, složena godišnja kamatna stopa može nam dati pogrešnu naznaku, jer se može dogoditi da tijekom prvih 15 godina ne zarađujemo, a svi prinosi dolaze u posljednjem razdoblju, Zarađivanje zarade tijekom 15 godina nije prihvatljivo za bilo koji posao koji treba održati.
Slično tome, ako dvije mogućnosti ulaganja imaju isti CAGR, može se dogoditi da je jedna privlačnija od druge zbog razloga što se rast u jednom događa u početnom razdoblju, dok se za ostale koncentrira na kraju razdoblje.
Relevantnost i upotreba sastavljene formule stope rasta godišnje
Složena godišnja stopa rasta zaista je korisna u izračunavanju prosječne stope rasta investicije i može pomoći u uspoređivanju različitih ulaganja. Kao što smo vidjeli u gornjem primjeru, godišnji rast investicija je neravnomjeran i nepristojan. Ali pomoću složene godišnje stope rasta, povrat se smanjuje. Drugi čimbenik koji složene godišnje stope rasta čini kritičnom metodom za određivanje rasta investicije jest to što uzima u obzir učinak složenstva, koji godišnja stopa povrata ne čini. Sastavljena godišnja stopa ne daje nam stvarnu sliku povrata jer samo izračunava prinos na glavnicu i zanemaruje kamate na komponentu kamate, ali to nije slučaj sa složenom godišnjom stopom rasta.
Sastavljeni kalkulator formule stope godišnjeg rasta
Možete koristiti sljedeći složen kalkulator godišnjeg rasta
| Iznos završne investicije | |
| Početni iznos | |
| Broj godina | |
| CAGR | |
| CAGR = | ((Završni iznos investicije / Početni iznos) 1 / Br. Godina -1) |
| = | ((0/0) 1/0 -1) = 0 |
Preporučeni članci
Ovo je vodič za formulu složenog godišnjeg rasta. Ovdje ćemo raspraviti kako izračunati CAGR zajedno s praktičnim primjerima. Također nudimo složen kalkulator godišnjeg rasta s učitavajućim Excel predložakom. Možete pogledati i sljedeće članke da biste saznali više -
- Vodič za formulu stope povrata
- Primjeri formule eksponencijalnog rasta
- Kalkulator za formulu teorema središnjeg ograničenja
- Kako izračunati tržišnu kapitalizaciju?