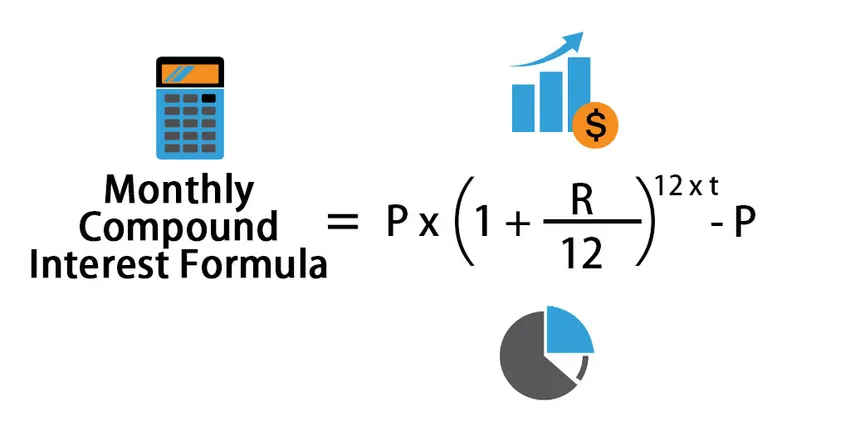
Mjesečna formula za složene kamate - Primjeri s predloškom Excela

Mjesečna formula za složene kamate (sadržaj)

• Formula
• Primjeri
• Kalkulator

Kakva je mjesečna formula za složene kamate?

Kada se određeni iznos novca posuđuje u određenom trajanju, a dodatni iznos treba platiti osim posuđenog iznosa. Tada se dodatni iznos koji plaćamo po fiksnoj stopi zove kamata. Složeni kamata je ukupna kamatna stopa koja uključuje izvornu kamatu i interes nove glavnice koja se razvija dodavanjem izvorne glavnice dospjeloj kamati. Za mjesečni složeni izračun, kamata koja je složen cijeli mjesec u cijeloj godini.

Mjesečna formula formule može se izračunati kao:

Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P

gdje,

• P = glavni iznos
• R = Stopa
• t = Vrijeme

Primjeri mjesečne formule složenih kamata (sa Excelovim predloškom)

Uzmimo primjer kako bismo bolje razumjeli izračun mjesečne složene kamate.

Možete preuzeti ovaj mjesečni obrazac Excel predloška za složene kamate ovdje - Mjesečni predložak formule Excela za mjesečne obrasce.

Mjesečna formula zanimanja za zajedničke primjere - Primjer br. 1

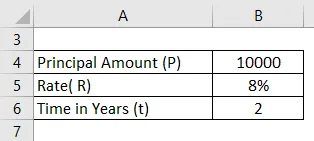
Zajmoprimac je pozajmio iznos od 10.000 Rs po stopi od 8%. Izračunajte mjesečnu složenu kamatnu stopu za 2 godine?

Riješenje:

Mjesečna složna kamata se izračunava pomoću donje formule

Mjesečna kamata za složene = P * (1 + (R / 12)) ^{12 * t} - P

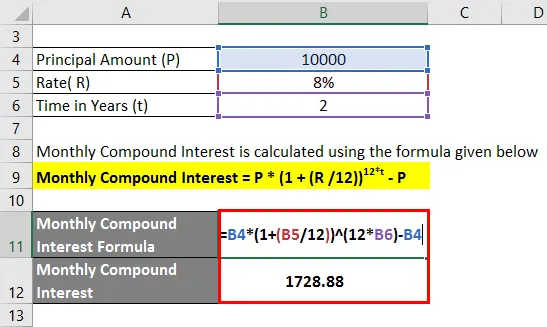
• Mjesečna složna kamata = 10 000 (1 + (8/12)) ^{2 * 12} - 10 000
• Mjesečna složna kamata = 1.728, 88

Mjesečna složena kamata za dvije godine iznosi 1.728, 88 Rs

Mjesečna formula kamate s obvezama - primjer # 2

Uloženi iznos novca po stopi od 10% iznosi 20 000 Rs. Kolika će biti mjesečna složena kamata za deset godina?

Riješenje:

Mjesečna složna kamata se izračunava pomoću donje formule

Mjesečna kamata za složene = P * (1 + (R / 12)) ^{12 * t} - P

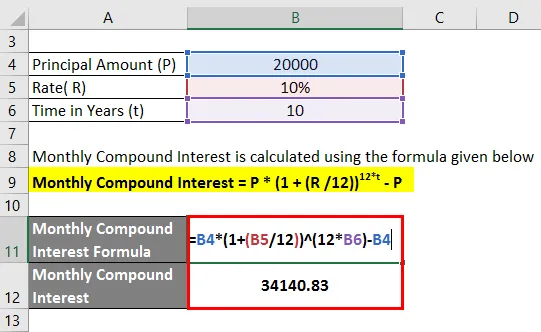
• Mjesečna složna kamata = 20.000 (1 + 10/12)) ^{10 * 12} - 20.000
• Mjesečna složna kamata = 34.140, 83

Mjesečna složena kamata za 10 godina iznosi 34.140, 83 Rs

Mjesečna formula zanimanja - primjer # 3

Gospođa Jefferson kupila je antički status za 500 dolara. Pet godina kasnije prodala je ovaj status za 800 dolara. Smatrala je to dijelom investicije. Izračunajte godišnju stopu koju je dobila?

Riješenje:

Ako razmislimo o ulaganju od 500 USD i dobit ćemo 800 USD u budućem razdoblju nakon t = 10 godina. Pretpostavljamo godišnju stopu m = 1 i implementiramo je u formulu.

A = P (l + r / m) ^mt

• 800 = 500 (1+ r / 1) ^{1 * 10}
• 800 = 500 (1 + r) ¹⁰

Sada smo za stopu (r) riješili u sljedećim koracima.

• 800 = 500 (1 + r) ¹⁰
• 8/5 = (1 + r) ¹⁰

Sada uzimamo snagu (1/10) na lijevoj strani jednadžbe i jasno je s desne strane.

• (8/5) ^1/10) = 1 + r

Izračunajte vrijednost s lijeve strane i riješite za r.

• 1.0481 = 1 + r
• 1.0481 - 1 = r
• 0, 0481 = r

Međutim, gospođa Jefferson zaradila je godišnju kamatnu stopu od 4, 81% što nije loša stopa povrata.

Obrazloženje

Složena kamata je proizvod početne glavnice za jedan plus godišnje kamatne stope povišene na broj složenih razdoblja minus jedan. Dakle, od rezultirajuće vrijednosti oduzima se početni iznos zajma.

Složene kamate mogu se izračunati kao:

Formula složenih kamata = (P (1 + i) ⁿ ) - P

Formula složenih kamata = (P (1 + i) ⁿ - 1)

Gdje:

• P = glavni iznos
• i = godišnja kamatna stopa u postotnim uvjetima
• n = složen razdoblja

Postoji određeni skup postupaka pomoću kojeg možemo izračunati mjesečnu kompoziciju.

Korak 1: Moramo izračunati iznos kamate dobiven korištenjem mjesečne kamate za kompenzaciju. Formula se može izračunati kao:

• A = (P (1 + i) ⁿ - 1) - P

2. korak: ako pretpostavimo da je kamatna stopa 5% godišnje. Prije svega, moramo izraziti vrijednost kamatne stope u ekvivalentni decimalni broj. To se može učiniti na sljedeći način.

• 5% = 5/100 = 0, 05

Korak 3: Budući da znamo da se kamata povećava mjesečno, pa možemo uzeti n = 12. Međutim, vremensko razdoblje je određeno u tom slučaju, smatrali bismo da je kredit uzet u razdoblju od jedne godine. Sada su kod nas dostupne sve varijable koje možemo izravno zamijeniti u formulu i iz nje dobiti rezultat.

• A = 1000 ((1 + 0, 05 / 12) ¹² - 1)
• A = 1000 ((1 + 0, 0042) ¹² - 1)
• A = 1000 ((1.0042) ¹² - 1)
• A = 1000 (1.0516 - 1)
• A = 1000 (0, 0516)
• A = 51, 6

Kamatnu stopu za 1 godinu izračunali smo mjesečnim sabiranjem oko 51, 6

Mjesečne složene kamate ne odražavaju primjetne promjene kada parkiramo određenu svotu novca za kratkotrajno trajanje. Razlog je taj što je trajalo nekoliko godina da složenje postigne primjetne promjene na snazi.

A najistaknutija stvar kod složenih kamata je da to čini da vaša ulaganja rastu brže od jednostavnih kamata. Što je češći vaš interval sažimanja, veća je razlika ili možemo reći da dnevni kamati za kompenzaciju ostvaruju više prihoda od vaših ulaganja od godišnje složene kamate za svaku danu kamatnu stopu.

Sljedeća tablica pokazuje razliku da se broj razdoblja složenivanja može stvoriti tijekom određenog razdoblja za zajam od 10 000 USD uz godišnju kamatnu stopu od 10% tijekom razdoblja od 12 godina.

Složena učestalost	Broj složenih razdoblja	Vrijednosti za i i n	Ukupne kamate
svake godine	1	I = 10%, n = 12	$ 21, 384.2837
Polu godišnje	2	I = 5%, n = 24	$ 22, 250.9994
tromjesečni	4	I = 2, 5%, n = 48	$ 22, 714.8956
Mjesečno	12	I = 0, 833%, n = 144	$ 23, 036.4896

Relevantnost i upotreba mjesečne formule složenih kamata

Složeni kamati pokazali su se boljim alatom za ulaganje, ali mogu biti vrlo opasni ako su primjenjivi na iznos vašeg kredita. Na kraju ćete platiti više kamata na iznos vašeg kredita.

Sklapanje postaje učinkovitije kada je vaše ulaganje bilo mjesečno ili tromjesečno umjesto godišnje jer daje bolji povrat. Ako posuđujete novac od bilo koje banke ili financijske institucije, tada je najbolja opcija godišnje slaganje. Kad posuđujete određenu svotu novca, tada će svakodnevno sačinjavanje biti produktivnije. Ali trebamo imati na umu, složeni postupci mogu biti povoljni ili nepovoljni ovisno o okolnostima.

Složeni kamati daju bolji povrat ulaganja, ovisi o roku i veličini ulaganja. Složeni interes raste brže nego što su vaša očekivanja.

Dobitak složenog kamata niže je naveden:

1. reinvestiranje
2. Bolji povrat ulaganja.
3. Dugoročna štednja.
4. Povećana zarada.

Kalkulator mjesečne kamate složenih kamata

Možete koristiti sljedeći mjesečni kalkulator formule složenih kamata

P
R
t
Mjesečna formula za složene kamate

Mjesečna formula kamate složenog =	P x ((1 + R / 12) 12 * t - P)
=	0 x ((1 +0/12) 12 * 0 - 0) = 0

Preporučeni članci

Ovo je vodič za mjesečnu formulu složenog kamata. Ovdje smo raspravljali o načinu izračunavanja mjesečne formule za zajedničke kamate zajedno s praktičnim primjerima. Također nudimo i mjesečni kalkulator za objedinjene kamate s besplatnim Excel predložakom koji možete preuzeti. Možete pogledati i sljedeće članke da biste saznali više -

1. Formula za složenu godišnju stopu rasta
2. Kako izračunati nominalnu kamatnu stopu?
3. Dnevna formula zanimanja
4. Vodič za Poissonovu formulu distribucije
5. Kamata vs Dividenda | 8 glavnih razlika koje biste trebali znati