
Harmonska srednja formula (Sadržaj)
- Harmonska srednja formula
- Primjeri harmonične srednje formule (sa Excelovim predloškom)
- Harmonični kalkulator srednje formule
Harmonska srednja formula
Harmonska sredina u osnovi je vrsta prosjeka koja se koristi u statistici koja je uzajamna aritmetička sredina recipročnih. Harmonska sredina je uvijek manja od aritmetičkih sredstava istog skupa podataka. Harmonska sredina se obično ne koristi kao aritmetička ili geometrijska sredina, a koristi se u specifičnim situacijama ili kada se radi o prosjecima jedinica, poput prosječne brzine putovanja i ostalih omjera. Ovo se također koristi u području financija za izračun množenja cijena poput omjera cijene i zarade, omjera cijene i prodaje, itd. Razlog za to je ako za izračun tih vrijednosti koristimo ponderiranu aritmetičku sredinu, a visoke podatkovne točke dobit će veću vagu i niže podatkovne točke dobit će manju težinu što će stvoriti problem i neće nam dati pravi višestruki.
Pretpostavimo da imamo skup podataka s n podatkovnih točaka, a zadaje ih X: (X1, X2, X3 …… ..Xn).
Formula za harmoničnu sredinu je
Harmonic Mean = n / (1/X1 + 1/X2 + 1/X3 ………… 1/Xn)
Gdje:
- X1, X2, … Xn - podatkovne točke
- n - Ukupan broj podataka
Koraci za izračunavanje harmonske srednje vrijednosti:
- Uzmite recipročnu vrijednost svih podataka u skupu podataka.
- Nakon toga pronađite prosjek / prosjek tih vrijednosti.
- Sljedeći i posljednji korak je uzvratiti tu vrijednost da bi se došlo do harmonične srednje vrijednosti.
Primjeri harmonične srednje formule (sa Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun Harmonične sredine.
Ovdje možete preuzeti ovaj Harmonski srednji predložak - Harmonični srednji predložakHarmonska srednja formula - Primjer br. 1
Recimo da imate skup podataka s 10 podatkovnih točaka i za to želimo izračunati harmoničnu sredinu.
Skup podataka: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
Recipročni će se izračunati kao:
Rezultat će biti naveden u nastavku.
Slično tome, moramo izračunati uzajamno za sve točke podataka.
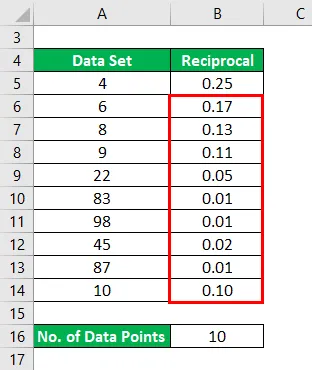
Srednja vrijednost uzajamnog izračunava se kao
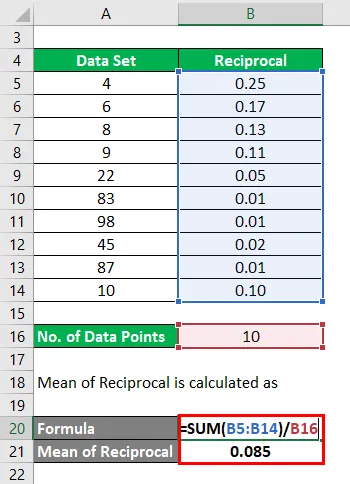
- Srednja vrijednost uzajamnog = (0, 25 + 0, 17 + 0, 13 + 0, 11 + 0, 05 + 0, 01 + 0, 01 + 0, 02 + 0, 01 + 0, 10) / 10
- Srednja vrijednost uzajamnog = 0, 85 / 10
- Srednja vrijednost uzajamnog = 0, 085
Harmonska srednja vrijednost izračunava se dolje opisanom formulom
Harmonska srednja = n / (1 / X1 + 1 / X2 + 1 / X3 ………… 1 / Xn)
Harmonska srednja vrijednost = 1 / srednja vrijednost uzajamnog
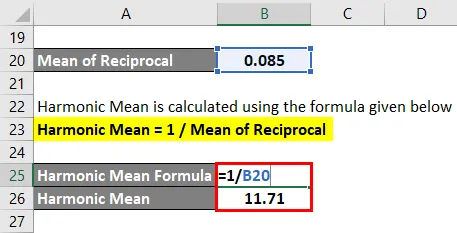
- Harmonska srednja vrijednost = 1 / 0, 085
- Harmonska srednja vrijednost = 11, 71
Harmonska srednja formula - Primjer br. 2
Sada pogledajte neke druge primjere iz praktičnog života kako biste jasnije shvatili značenje i uvidite razliku između aritmetičke i harmonične srednje vrijednosti.
Recimo da vozite automobil i putujete u neki drugi grad. Ukupno vrijeme za vaše putovanje je 4 sata, od čega vozite brzinom od 60 km / sat tijekom prvog sata, 50 km / sat tijekom drugog sata, 100 km / sat tijekom trećeg sata i 40 km / sat tijekom 4. sat.
Dakle, prosječnu brzinu možete izračunati jednostavnim srednjim brojem:
- Prosječna brzina = (60 + 50 + 100 + 40) / 4
- Prosječna brzina = 250/4
- Prosječna brzina = 62, 5 km / sat
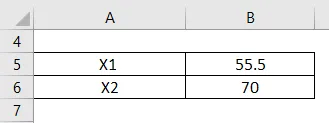
No, recimo da je podatak da ste u prvoj polovici vremena vozili brzinom od 55, 5 km / sat, a sljedeću polovicu brzinom od 70 km / sat. U tom slučaju moramo upotrijebiti harmoničnu sredinu kako bismo pronašli prosječnu brzinu.
Harmonska srednja vrijednost izračunava se dolje opisanom formulom
Harmonska srednja = n / (1 / X1 + 1 / X2 + 1 / X3 ………… 1 / Xn)
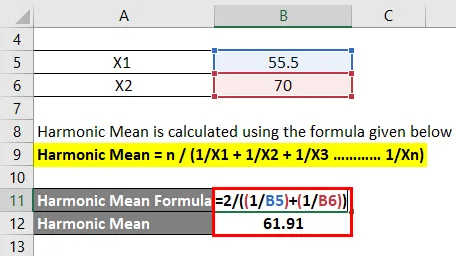
- Harmonska srednja vrijednost = 2 / ((1 / 55, 5) + (1/70))
- Harmonska srednja vrijednost = 61, 91 km / sat
Ako vidite ovdje, vrijednost harmonične srednje vrijednosti je manja od prostog prosjeka.
Obrazloženje
Iako se harmonička sredina u osnovi koristi za pronalaženje prosjeka skupa podataka, poput jednostavne aritmetičke srednje vrijednosti, ona se ne izračunava kao jednostavno aritmetička sredina. Ako imamo veliki skup podataka, izračunavanje harmonijske srednje vrijednosti postaje složeno i dugotrajno. Sa složenošću dolazi do zbrke i šanse za pogrešku. Stoga treba biti vrlo oprezan pri proračunu harmonijske srednje veličine velikog broja podataka. Kako uzimamo recipročno u proračunu harmoničke srednje vrijednosti, najveća težina se daje najnižoj vrijednosti i obrnuto. Ponekad to nije potrebno.
Drugi nedostatak je taj što ako je bilo koja podatkovna točka u skupu podataka jednaka 0, harmonska srednja vrijednost ne može se izračunati s obzirom da x / 0 nije definirano. Na neki način, harmonska sredina ima vrlo ograničen domet za razliku od aritmetičke srednje. Također, ovo je izuzetno osjetljivo prema odmetnicima i ekstremnim vrijednostima.
Relevantnost i upotreba harmonske srednje formule
Vidjeli smo višestruka ograničenja harmonskih sredina i to je razlog što nema mnogo praktične primjene. Ali postoje i neke koristi i pozitivne točke. Harmonska sredina je strogo definirana i zbog toga je pogodna za daljnje matematičke operacije. Također, za razliku od geometrijske srednje vrijednosti, na to ne utječu fluktuacije uzorkovanja. Budući da daje malu težinu malim skupovima podataka, što je ponekad poželjno kako podaci ne bi bili pristrani prema visokim vrijednostima. Situacije koje uključuju vrijeme i stope, harmonična sredina daju bolje i preciznije rezultate od jednostavne srednje vrijednosti.
Rečeno i učinjeno, harmonična sredina ima nekoliko prednosti, ali s obzirom da ima ograničen opseg, a nedostaci su mu više, ne koristi se često i ima ograničenu prisutnost.
Harmonični kalkulator srednje formule
Možete koristiti sljedeći Harmonski kalkulator srednje vrijednosti
| n | |
| X1 | |
| X2 | |
| X3 | |
| Harmonska srednja formula | |
| Harmonska srednja formula = |
|
|
Preporučeni članci
Ovo je vodič za Harmoničnu srednju formulu. Ovdje ćemo raspraviti kako izračunati harmoničnu sredinu zajedno s praktičnim primjerima. Također nudimo Harmonic Prosečni kalkulator s mogućnošću skidanja Excel predloška. Možete pogledati i sljedeće članke da biste saznali više -
- Vodič za raspon formule
- Najbolji primjeri formule vremena za udvostručavanje
- Kalkulator za formulu potonućeg fonda
- Kako izračunati DPMO?