Linearna regresija u Excelu - Kako napraviti linearnu regresiju u Excelu?

Linearna regresija u Excelu (Sadržaj)

Uvod u linearnu regresiju u Excelu
Metode korištenja linearne regresije u Excelu

Uvod u linearnu regresiju u Excelu

Linearna regresija je statistička tehnika / metoda koja se koristi za proučavanje odnosa dvije kontinuirane kvantitativne varijable. U ovoj se tehnici neovisne varijable koriste za predviđanje vrijednosti ovisne varijable. Ako postoji samo jedna neovisna varijabla, onda je to jednostavna linearna regresija, a ako je broj neovisnih varijabli više od jedne, onda je to višestruka linearna regresija. Modeli linearne regresije imaju odnos između ovisnih i neovisnih varijabli postavljanjem linearne jednadžbe u promatrane podatke. Linearno se odnosi na činjenicu da koristimo liniju kako bi odgovarala našim podacima. Ovisne varijable koje se koriste u regresijskoj analizi nazivaju se i reakcijskim ili predviđenim varijablama, a neovisne varijable također se nazivaju objašnjenja ili prediktori.

Linearna regresijska linija ima jednadžbu vrste: Y = a + bX;

Gdje:

X je objasnjavajuća varijabla,
Y je ovisna varijabla,
b je nagib linije,
a je presijecanje y (tj. vrijednost y kada je x = 0).

Metoda najmanje kvadrata općenito se koristi u linearnoj regresiji koja izračunava najbolju liniju za promatrane podatke minimizirajući zbroj kvadrata odstupanja podatkovnih točaka od crte.

Metode korištenja linearne regresije u Excelu

Ovaj primjer vas uči metodama za izvršavanje linearne regresijske analize u Excelu. Pogledajmo nekoliko metoda.

Ovdje možete preuzeti ovaj Linear Regression Excel predložak ovdje - Linear Regression Excel predložak

Metoda br. 1 - Rješavanje crteža s trendom

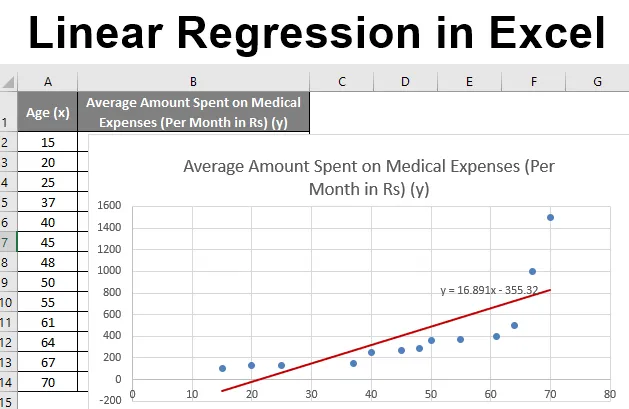
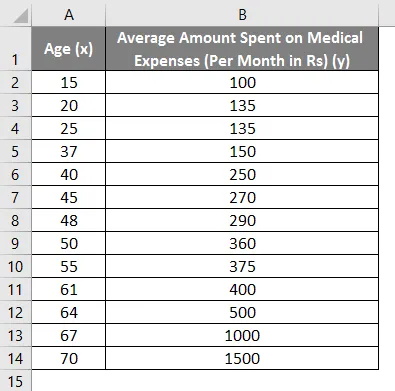
Recimo da imamo skup podataka o pojedincima s njihovom dobi, indeksom biološke mase (BMI) i iznosom koji su potrošili na medicinske troškove u mjesec dana. Sada, sa uvidom u osobine pojedinaca kao što su dob i BMI, želimo pronaći kako ove varijable utječu na medicinske troškove, te ih stoga koristiti za provođenje regresije i procjenu / predviđanje prosječnih medicinskih troškova nekih određenih osoba. Pogledajmo prvo kako samo dob utječe na troškove liječenja. Pogledajmo skup podataka:

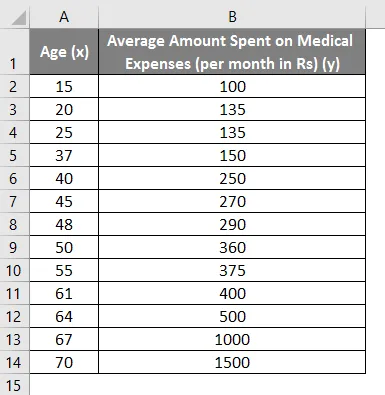
Iznos za medicinske troškove = b * dob + a

Odaberite dva stupca skupa podataka (x i y), uključujući zaglavlja.

Kliknite na "Umetanje" i proširite padajući izbornik za "Scatter Chart" i odaberite sličicu "Scatter" (prva)

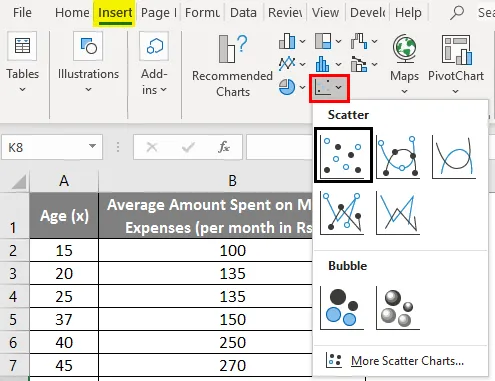
Sada će se pojaviti crta raspršenja i na tome bismo nacrtali regresijsku crtu. Da biste to učinili, desnom tipkom miša kliknite bilo koju točku podataka i odaberite "Dodaj trend"

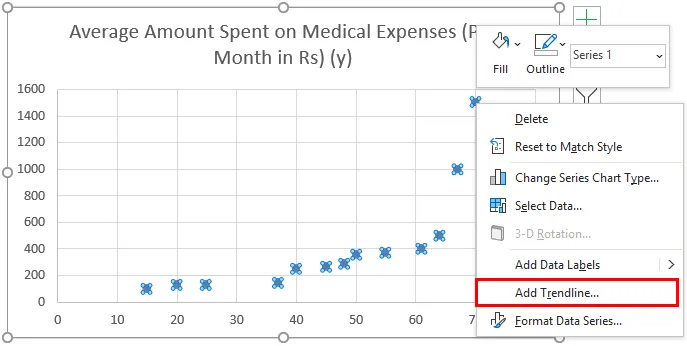
Sada u oknu "Obliku trendovske linije" s desne strane odaberite "Linearna linija trenda" i "Prikaži jednadžbu na grafikonu".

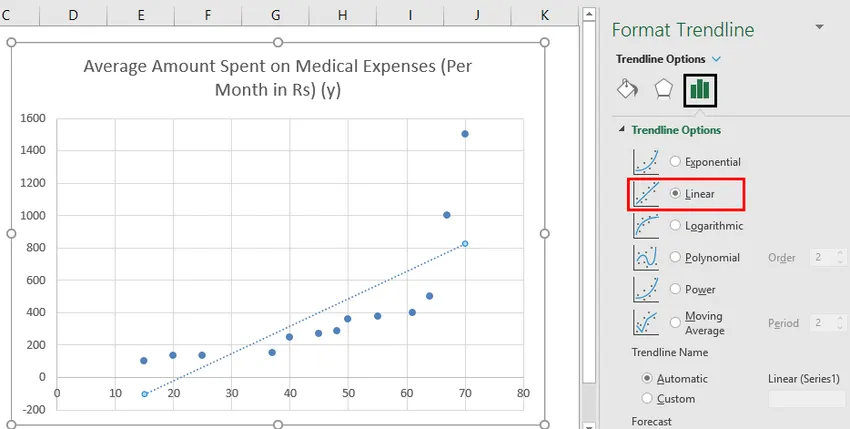
Odaberite "Prikaži jednadžbu na grafikonu".

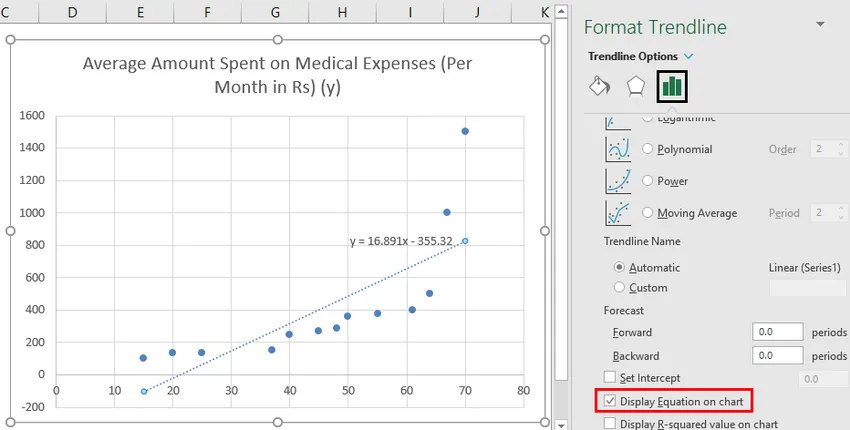
Možemo improvizirati grafikon prema našim zahtjevima, poput dodavanja naslova osi, mijenjanja razmjera, boje i vrste crta.

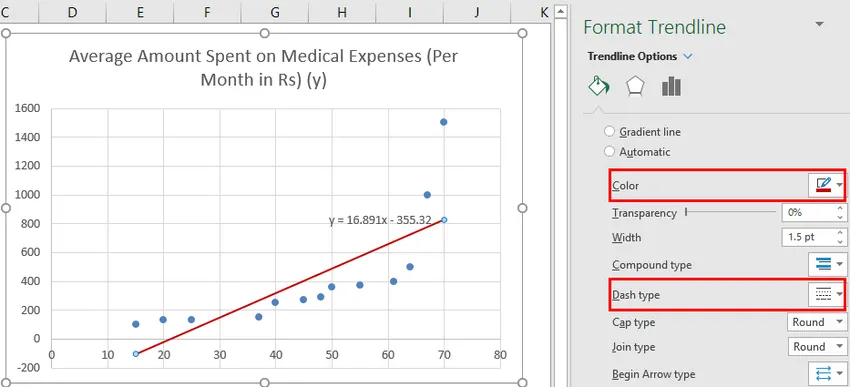
Nakon improvizacije grafikona ovo je rezultat koji dobivamo.

Napomena: U ovoj vrsti regresijskog grafikona ovisna varijabla uvijek treba biti na y-osi, a nezavisna na x-osi. Ako se graf crta obrnutim redoslijedom, tada prebacite osi u grafikon ili zamijenite stupce u skupu podataka.

2. metoda - metoda dodavanja ToolPak analize

Analysis ToolPak ponekad nije omogućen prema zadanim postavkama i to trebamo učiniti ručno. Učiniti tako:

Kliknite izbornik "Datoteka".

Nakon toga kliknite na 'Opcije'.

Odaberite "Excel dodaci" u okviru "Upravljanje" i kliknite "Idi"

Odaberite "Analysis ToolPak" -> "OK"

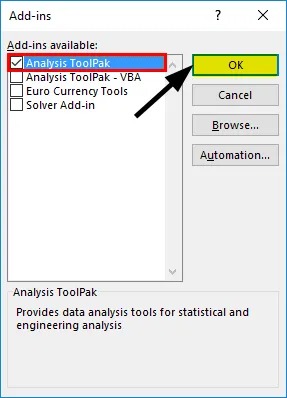
To će dodati alate 'Analiza podataka' na karticu 'Podaci'. Sada pokrećemo regresijsku analizu:

Kliknite "Analiza podataka" na kartici "Podaci"

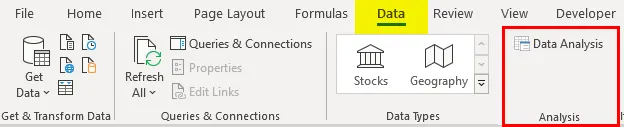
Odaberite "Regresija" -> "OK"

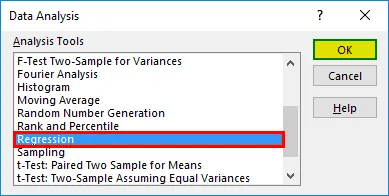
Pojavit će se dijaloški okvir za regresiju. Odaberite raspon unosa Y i raspon ulaza X (medicinski troškovi i dob, respektivno). U slučaju višestruke linearne regresije, možemo odabrati više stupaca neovisnih varijabli (poput ako želimo vidjeti utjecaj BMI-a i na medicinske troškove).
Potvrdite okvir "Oznake" da biste uključili zaglavlja.
Odaberite željenu opciju "output".
Označite potvrdni okvir "zaostaci" i kliknite "U redu".

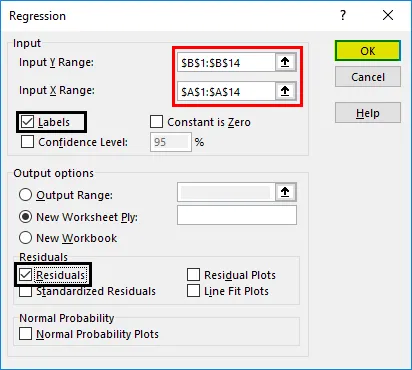
Sada će se naš rezultat regresijske analize stvoriti u novom radnom listu, navodeći regresijsku statistiku, ANOVA, ostatke i koeficijente.

Izlazno tumačenje:

Regresijska statistika govori koliko se jednadžba regresije uklapa u podatke:

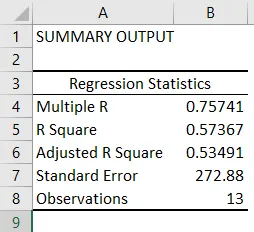
Multiple R je koeficijent korelacije koji mjeri snagu linearnog odnosa između dvije varijable. Leži između -1 i 1, a njegova apsolutna vrijednost prikazuje snagu odnosa s velikom vrijednošću koja označava jači odnos, niska vrijednost koja označava negativnu i nulta vrijednost koja pokazuje da nema odnosa.
R Square je koeficijent odlučnosti koji se koristi kao pokazatelj dobrog fitanja. Leži između 0 i 1, a vrijednost blizu 1 označava da se model dobro uklapa. U ovom slučaju, 0, 57 = 57% y-vrijednosti objašnjava se x-vrijednostima.
Prilagođeni R kvadrat R je podešen za broj prediktora u slučaju višestruke linearne regresije.
Standardna pogreška prikazuje preciznost regresijske analize.
Promatranja prikazuju broj opažanja modela.
Anova govori o razini varijabilnosti unutar regresijskog modela.

To se obično ne koristi za jednostavnu linearnu regresiju. Međutim, "F-značajnost" pokazuje koliko su naši rezultati pouzdani, čija vrijednost veća od 0, 05 sugerira odabir drugog prediktora.

Koeficijenti je najvažniji dio koji se koristi za izgradnju regresijske jednadžbe.

Dakle, naša bi regresijska jednadžba bila: y = 16.891 x - 355.32. To je isto kao što je učinjeno metodom 1 (rasipanje grafikona s trend-linijom).

Sada ako želimo predvidjeti prosječne troškove liječenja kada je starosna dob 72:

Dakle, y = 16.891 * 72 -355.32 = 860.832

Na taj način možemo predvidjeti vrijednosti y za bilo koje druge vrijednosti x.

Ostaci pokazuju razliku između stvarnih i predviđenih vrijednosti.

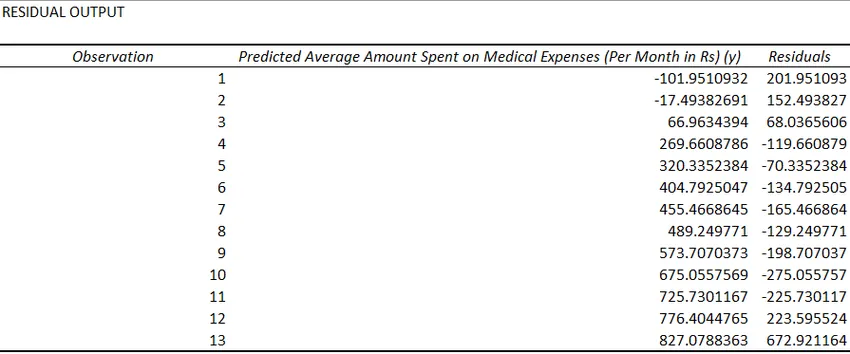
Posljednja metoda regresije nije toliko često korištena i zahtijeva statističke funkcije poput nagiba (), presretanja (), korela () itd. Za provođenje regresijske analize.

Stvari koje treba zapamtiti o linearnoj regresiji u Excelu

Regresijska analiza se općenito koristi da se utvrdi postoji li statistički značajna veza između dva skupa varijabli.
Koristi se za predviđanje vrijednosti ovisne varijable na temelju vrijednosti jedne ili više neovisnih varijabli.
Kad god želimo linearni regresijski model uklopiti u skupinu podataka, tada treba pažljivo promatrati raspon podataka kao da koristimo jednadžbu regresije za predviđanje bilo koje vrijednosti izvan ovog raspona (ekstrapolacija), tada to može dovesti do pogrešnih rezultata.

Preporučeni članci

Ovo je vodič za Linearnu regresiju u Excelu. Ovdje smo raspravljali o tome kako napraviti linearnu regresiju u Excelu zajedno s praktičnim primjerima i besplatnim Excelovim predloškom. Možete i pregledati naše druge predložene članke -