
Formula pogrešaka (Sadržaj)
- Formula pogreške
- Primjeri margine formule pogreške (sa Excelovim predloškom)
- Granica greške Kalkulator formule
Formula pogreške
U statistici, izračunavamo interval pouzdanosti da vidimo gdje će vrijednost podataka statističkih uzoraka pasti. Raspon vrijednosti koje su ispod i iznad statistike uzorka u intervalu pouzdanosti poznat je pod nazivom Granica pogreške. Drugim riječima, u osnovi je stupanj pogreške u statistici uzorka. Što je veća granica pogreške, to će manje vjerovati u rezultate jer je stupanj odstupanja u tim rezultatima vrlo visok. Kao što mu ime govori, greška je raspon vrijednosti iznad i ispod stvarnih rezultata. Na primjer, ako dobijemo odgovor u anketi u kojoj je 70% ljudi odgovorilo „dobro“, a greška je 5%, to znači da općenito 65% do 75% stanovništva misli da je odgovor „dobar“,
Formula za marginu pogreške -
Margin of Error = Z * S / √n
Gdje:
- Z - Z bod
- S - Standardno odstupanje stanovništva
- n - Veličina uzorka
Druga formula za izračunavanje pogreške je:
Margin of Error = Z * √((p * (1 – p)) / n)
Gdje:
- p - uzorak proporcija (djelić uspješnog uzorka)
Da biste pronašli željeni z rezultat, morate znati interval pouzdanosti uzorka, jer Z ocjena ovisi o tome. Ispod tablice je prikazan odnos intervala pouzdanosti i z rezultata:
| Interval pouzdanosti | Z - Ocjena |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Nakon što prepoznate interval pouzdanosti, možete upotrijebiti odgovarajuću vrijednost z i od tamo izračunati granicu pogreške.
Primjeri margine formule pogreške (sa Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun marže pogreške.
Ovdje možete preuzeti ovaj predložak margine pogreške - Predložak margine pogreškeFormula pogreške margine - Primjer br. 1
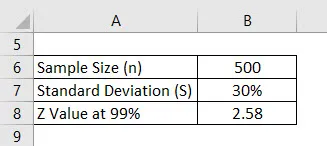
Recimo da provodimo anketu kako bismo vidjeli kakva je ocjena ocjena sveučilišnih studenata. Nasumično smo odabrali 500 učenika i pitali ih ocjenu. Prosjek toga je 2, 4 od 4, a standardno odstupanje je 30%. Pretpostavimo da je interval pouzdanosti 99%. Izračunajte granicu pogreške.
Riješenje:
Margin of Error izračunava se pomoću donje formule
Margina pogreške = Z * S / √n
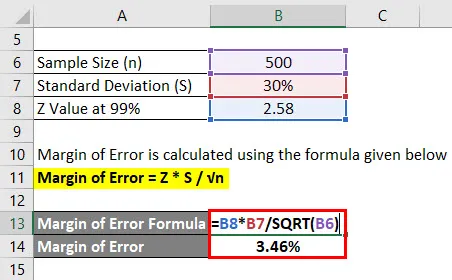
- Pogreška = 2, 58 * 30% / √ (500)
- Razlika pogreške = 3, 46%
To znači da je sa 99% samopouzdanja prosječna ocjena učenika 2, 4 plus ili minus 3, 46%.
Formula pogreške margine - Primjer br. 2
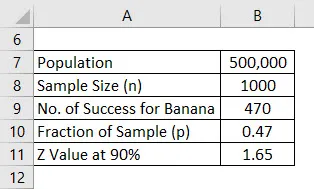
Recimo da lansirate novi zdravstveni proizvod na tržište, ali zbunjeni ste koji će okus voljeti ljude. Zbunjeni ste između arome banane i vanilije i odlučili ste provesti istraživanje. Vaša populacija za to je 500 000, što je vaše ciljno tržište, a izvan toga ste odlučili pitati mišljenje 1000 ljudi i to će biti uzorak. Pretpostavimo da je interval pouzdanosti 90%. Izračunajte granicu pogreške.
Riješenje:
Nakon što je anketa provedena, saznali ste da se 470 ljudi svidjelo okusu banane, a 530 je zatražilo aromu vanilije.
Margin of Error izračunava se pomoću donje formule
Margina pogreške = Z * √ ((p * (1 - p)) / n)
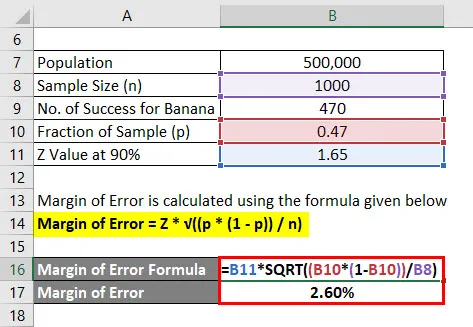
- Margina pogreške = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Razlika pogreške = 2, 60%
Dakle, možemo reći da je s 90% pouzdanosti da je 47% svih ljudi voljelo okus banane plus ili minus 2.60%.
Obrazloženje
Kao što je gore spomenuto, pogreška nam pomaže da shvatimo je li veličina uzorka vašeg istraživanja odgovarajuća ili ne. U slučaju da je pogreška marže prevelika, može se dogoditi da je naša veličina uzorka premala i to moramo povećati tako da se rezultati uzorka poklapaju s rezultatima populacije.
Postoje neki scenariji u kojima granica pogreške neće biti od velike koristi i neće nam pomoći u praćenju pogreške:
- Ako pitanja ankete nisu osmišljena i ne pomažu u traženju odgovora
- Ako osobe koje reagiraju na anketu imaju pristranosti u vezi s proizvodom za koji se anketa vrši, tada također rezultat nije baš točan
- Ako je sam odabrani uzorak odgovarajući predstavnik populacije, u tom slučaju će i rezultati biti na pretek.
Također, jedna je velika pretpostavka da je stanovništvo normalno raspodijeljeno. Dakle, ako je veličina uzorka premala i distribucija stanovništva nije normalna, z rezultat se ne može izračunati i nećemo moći pronaći marginu pogreške.
Relevantnost i upotreba margine pogreške
Kad god koristimo uzorke podataka da bismo pronašli odgovarajući odgovor za skup stanovništva, postoji izvjesna nesigurnost i šanse da bi rezultat mogao odstupiti od stvarnog rezultata. Granica pogreške će nam reći da je razina uzorka takva kakva je razina odstupanja. Moramo smanjiti granicu pogreške kako bi naši uzorci prikazali stvarnu priču o podacima stanovništva. Dakle, što je niža granica pogreške, bolji će biti i rezultati. Granica pogreške dopunjava i upotpunjava statističke podatke koje imamo. Na primjer, ako se anketom utvrdi da 48% ljudi radije provodi vrijeme kod kuće tijekom vikenda, ne možemo biti toliko precizni i u tim podacima postoje neki elementi koji nedostaju. Kada smo ovdje uveli granicu pogreške, recimo, 5%, tada će se ishod tumačiti kao da se 43-53% ljudi svidjelo ideji da budu kod kuće tijekom vikenda, što ima potpuno smisla.
Granica greške Kalkulator formule
Možete koristiti sljedeću maržu greške Kalkulator
| Z | |
| S | |
| √n | |
| Pogreška | |
| Pogreška | = |
|
|
Preporučeni članci
Ovo je vodič za formulu Margin of Error. Ovdje smo raspravljali o tome kako izračunati maržu pogreške zajedno s praktičnim primjerima. Također nudimo kalkulator Margin of Error s predloškom Excel kojeg možete preuzeti. Možete pogledati i sljedeće članke da biste saznali više -
- Vodič prema formuli amortizacije pravih linija
- Primjeri dvostruke formule vremena
- Kako izračunati amortizaciju?
- Formula za teorem o središnjoj granici
- Altman Z ocjena | Definicija | Primjeri
- Formula amortizacije | Primjeri s predloškom Excela