Složeni brojevi u MATLAB - Kako generirati složeni broj?

Uvod u složene brojeve u MATLAB-u

Složeni brojevi su kombinacija stvarnih brojeva i imaginarnih brojeva u obliku p + qi gdje su p i q stvarni brojevi, a i je imaginarni broj. Definiran je imaginarni broj gdje je i rezultat jednadžbe a 2 = -1. Možemo koristiti i ili j za označavanje imaginarnih jedinica. Kako se složeni brojevi koriste u bilo kojem matematičkom proračunu, a Matlab se uglavnom koristi za obavljanje matematičkih izračuna. Dakle, složeni brojevi predstavljaju važan dio učenja Matlaba.

Generacija složenih brojeva u MATLAB-u

Složeni brojevi mogu se stvoriti ili deklarirati u Matlabu pomoću 'složene' funkcije. Također možemo stvoriti složene brojeve pronalaženjem kvadratnog korijena bilo kojeg negativnog broja. U Matlabu možemo upotrijebiti i ili j da označimo imaginarni dio složenog broja.

Primjeri

X = 4 + 5i

Ovdje je X složen broj koji sadrži 2 dijela tj. Stvarni i imaginarni dio. 4 je stvarni dio i 5 je imaginarni dio. Prave i imaginarne dijelove možemo pronaći pomoću funkcija u Matlabu.

a = real (X) = 4 (ovo daje stvarni dio složenog broja)
b = imag (X) = 5 (Ovo daje imaginarni dio složenog broja)
kompleks (6, 7) = 6 + 7i (Ova se funkcija koristi za stvaranje složenog broja)

U Matlabu također možemo stvoriti složene nizove koji se mogu deklarirati pomoću složenih funkcija.

a = složen (x, y)

Postoje određeni uvjeti za x i y koje bismo trebali slijediti kao x, a y ne bi trebali biti jednokračni ili dvostruki. Može se stvoriti složeni skalar ako su dva ulaza skalarne naravi poput,

X = složen (5, 3)
X = 5.0000 + 3.0000i

Slično tome, složeni vektor može se stvoriti ako imamo dva ulaza kao vektori.

X = uint8 ((4, 5, 6, 7));
Y = uint8 ((3 5 1; 2));
a = složen (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Možemo stvoriti složen broj koji ima samo jedan skalar poput,

X = složen (10)
X = 10, 0000 + 0, 0000i

Postoje određeni uvjeti kojih se sljedeći argumenti ulaza i izlaza trebaju slijediti,

Ulazni argumenti sadrže stvarne i imaginarne dijelove poput x bilo kojeg y. x i y trebaju biti skalarni, vektorski, višedimenzionalni niz ili matrica u MATLAB-u. x i y veličina bi trebala biti jednaka. Trebali bi biti istog tipa podataka, ali postoji nekoliko izuzetaka poput dvostrukog može se koristiti s jednostrukim, a cijeli broj se može kombinirati s dvostrukim, što je skalarno.

Izlaz niza može biti vektorski, skalarni, matrični ili višedimenzionalni niz ovisno o ulaznim argumentima. Veličina izlaza mora biti ista kao i ulaza. Ako su ulazni argumenti različitih vrsta podataka, a izlaz se određuje,

Ako je bilo koji od ulaznih argumenata pojedinačni po prirodi, izlaz bi također trebao biti jedinstven.
Ako je bilo koji od ulaznih argumenata cjelobrojni u prirodi, izlaz bi trebao biti cijeli tip podataka.

Pomoću izrealne funkcije možemo provjeriti je li matrica stvarna ili imaginarna.

Kodirati:

X = (2+i, 1); Isreal(X)

Izlaz:

Kodirati:

Isreal (X (2))

Izlaz:

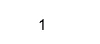
Da bismo izvukli stvarne i imaginarne dijelove, u Matlabu možemo koristiti stvarne i imag funkcije,

Kodirati:

real(X)

Izlaz:

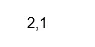
Kodirati:

imag(X)

Izlaz:

Operacije i funkcije složenih brojeva u MATLAB-u

Postoji nekoliko operacija i funkcija koje se mogu obavljati korištenjem složenih brojeva poput Matlaba

abs: Ova se funkcija koristi za pronalaženje modula bilo kojeg složenog broja u obliku p + qi. aps (2 + 3i) = kvadratni korijen od (2 2 + 3 2) = (13) 0, 5
kut: Za pronalaženje faznog ugla složenog broja.

Postoje određeni savjeti koje treba slijediti za pravilno funkcioniranje složenih brojeva u Matlabu poput,

Trebali bismo izbjegavati korištenje i i j kao dijela bilo kojih imena varijabli jer se koriste u označavanju imaginarnih dijelova složenog broja.
Treba izbjegavati upotrebu j ili i ako je imaginarni dio 1. Umjesto toga, možemo upotrijebiti 1j ili 1i.
Možemo stvoriti složenu funkciju u Matlabu kada se i i j u nekom dijelu koriste kao imena varijabli, argumenti unosa nisu jednostruki ili dvostruki, a imaginarni dio je nula.

Zaključak

Složeni brojevi koriste se u matematičkom ili inženjerskom području. Mnoge se stvarne ili praktične aplikacije mogu opisati pomoću zamišljenog dijela složenih brojeva. Dakle, razumijevanje upotrebe i primjene složenih brojeva na različitim platformama važno je, posebno ako se bavite bilo kojom fizičkom ili matematičkom domenom.

Preporučeni članci

Ovo je vodič za složene brojeve u MATLAB-u. Ovdje ćemo raspravljati o uvođenju i složenom generiranju broja u matlabu, uključujući njegove primjere s radom i funkcijom. Možete pogledati i sljedeće članke da biste saznali više -