Formula za očekivani povratak (Sadržaj)
- Formula za očekivani povratak
- Primjeri formula očekivanog povratka (s Excelovim predloškom)
- Kalkulator formule očekivanog povratka
Formula za očekivani povratak
Očekivani povrat može se definirati kao vjerojatni prinos za portfelj koji ulažu investitori na temelju prošlih povrata ili se može definirati i kao očekivana vrijednost portfelja na temelju raspodjele vjerojatnih prinosa.
Evo formule za očekivani povratak -
Expected Return = Expected Return=∑ (R i * P i )
Gdje
- R i - Očekivanje povrata svakog scenarija
- P i - Vjerojatnost povratka u tom scenariju
- i - Mogući scenariji koji se protežu od 1 do n
Primjeri formula očekivanog povratka (s Excelovim predloškom)
Uzmimo primjer kako bismo bolje razumjeli izračun formule Očekivani povrat.
Formula za očekivani povratak - Primjer # 1
Uzmimo primjer portfelja dionica i obveznica gdje dionice imaju 50% težine, a obveznice 50%. Očekivani povrat dionica je 15%, a očekivani povrat obveznica 7%.
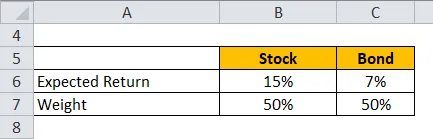
Očekivani povrat izračunava se niže prikazanom formulom
Očekivani povrat za portfelj = Težina zaliha * Očekivani povrat za dionicu + Težina obveznice * Očekivani povrat za obveznicu
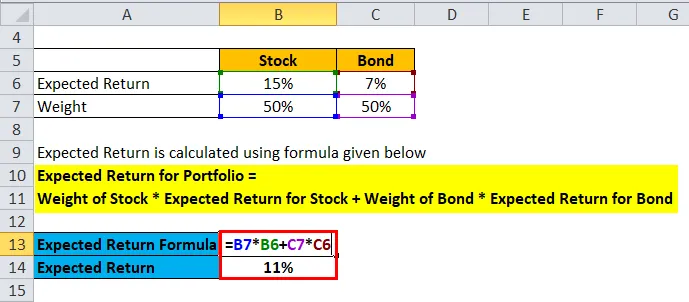
- Očekivani povrat za portfelj = 50% * 15% + 50% * 7%
- Očekivani povrat za portfelj = 7, 5% + 3, 5%
- Očekivani povrat za portfelj = 11%
Formula za očekivani povratak - Primjer # 2
Uzmimo primjer portfelja koji ima dionice Reliance, Tata Steel, Eicher Motors i ITC.
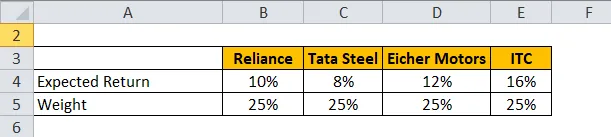
Očekivani povrat izračunava se niže prikazanom formulom
Očekivani povrat za portfelj = ∑ Težina svake dionice * Očekivani povrat za svaku dionicu

- Očekivani povrat za portfelj = 25% * 10% + 25% * 8% + 25% * 12% + 25% * 16%
- Očekivani povrat za portfelj = 2, 5% + 2% + 3% + 4%
- Očekivani povrat za portfelj = 11, 5%
Formula za očekivani povratak - Primjer # 3
Uzmimo primjer portfelja državnih obveznica HUL, HDFC i 10 godina.
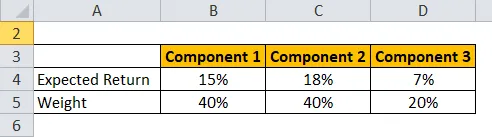
Očekivani povrat izračunava se niže prikazanom formulom
Očekivani povrat za portfelj = ∑ Težina svake komponente * Očekivani povrat za svaku komponentu
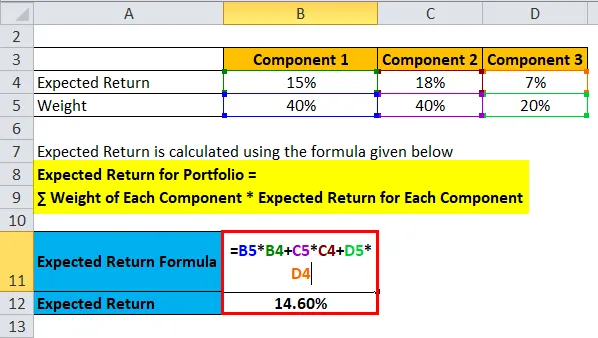
- Očekivani povrat za portfelj = 40% * 15% + 40% * 18% + 20% * 7%
- Očekivani povrat za portfelj = 6% + 7, 2% + 1, 40%
- Očekivani povrat za portfelj = 14, 60%
Ovdje možete preuzeti ovaj Excel predložak Formule za očekivani povratak - Predložak Excela Formula za povratak
Objašnjenje formule očekivanog povratka
Očekivani povrat može se definirati kao vjerojatni prinos za portfelj koji ulažu investitori na temelju prošlih povrata ili se može definirati i kao očekivana vrijednost portfelja na temelju raspodjele vjerojatnih prinosa. Očekivani povrat može se kratkoročno posmatrati kao slučajna varijabla koja može uzeti različite vrijednosti na temelju nekih različitih vjerojatnosti. Ova slučajna varijabla ima vrijednosti unutar određenog raspona i može uzimati vrijednosti samo u tom određenom rasponu. Stoga se izračun očekivanog prinosa temelji na povijesnim podacima i stoga možda nije pouzdan u predviđanju budućih povrata. Može se promatrati kao mjerilo različitih vjerojatnosti i vjerojatnosti dobivanja pozitivnog prinosa na nečijem ulaganju i vrijednosti tog povrata.
Svrha toga je dati investitoru ideju za različitu razinu rizika. Koji su različiti scenariji s različitim vjerojatnostima koji će donijeti mogući povrat veći od povrata bez rizika. Kao što svi znamo, povrat bez rizika bio bi 10-godišnji prinos državnih obveznica Vlade Sjedinjenih Država.
Relevantnost i upotreba formule očekivanog povratka
Kao što je gore spomenuto, izračunavanje očekivanog povrata temelji se na povijesnim podacima i stoga ima ograničenje predviđanja budućih mogućih povrata. Ulagači moraju imati na umu razne druge čimbenike i ne ulagati na temelju izračunatog očekivanog povrata. Primjer:
Portfelj A - 10%, 12%, -9%, 2%, 25%
Portfolio B - 9%, 7%, 6%, 6%, 12%
Ako uzmemo u obzir oba gornja portfelja, očekujemo da će oba dobiti 8%, ali portfelj A pokazuje puno rizika zbog velike razlike u prinosu. Stoga investitori moraju uzeti u obzir ovaj rizik koji se izračunava mjerama kao što su Standardno odstupanje i varijanca.
- Varijanca - može se definirati kao varijacija skupa podataka danih oko njihove srednje vrijednosti. Izračunava se na temelju vjerojatnosti ponderiranog prosjeka kvadratnih odstupanja od srednje vrijednosti. To je mjera rizika koju investitori moraju uzeti u obzir.
Prvo treba izračunati sredinu svih prinosa. Potom se odstupanje svakog povratka utvrđuje od glavne vrijednosti i prikazuje se kvadratom kako bi se osigurali svi pozitivni rezultati. A kad su kvadratni, oni se množe s odgovarajućim vrijednostima vjerojatnosti da bi se otkrila varijanca.
Varijanta portfelja može se izračunati iz sljedeće formule: - ako postoje dva portfelja A i B
Varijanta portfelja = w A 2 * σ A 2 + w B 2 * σ B 2 + 2 * w A * w B * Cov (A, B)
Gdje je Cov (A, B) - kovarijacija portfelja A i B
- Standardno odstupanje - To je još jedna mjera koja označava odstupanje od njegove srednje vrijednosti. Standardno odstupanje se izračunava uzimajući kvadratni korijen varijance i označavano sa σ.
Kalkulator formule očekivanog povratka
Možete koristiti sljedeći kalkulator očekivanog povrata.
| R 1 | |
| P 1 | |
| R 2 | |
| P 2 | |
| R 3 | |
| P 3 | |
| R 4 | |
| P 4 | |
| Očekivani povratak | |
| Očekivani povrat = | R 1 * P 1 + R 2 * P 2 + R 3 * P 3 + R 4 * P 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Zaključak
Očekivani povrat može se definirati kao vjerojatni povrat portfelja ulagača na temelju prošlih povrata. Kako se koristi samo prošli povrat, to ograničenje i vrijednost očekivanog povrata ne bi trebali biti jedini čimbenik koji investitori razmatraju u odlučivanju da li ulagati u portfelj ili ne. Postoje i druge mjere koje je potrebno razmotriti, poput varijance portfelja i standardnog odstupanja.
Preporučeni članci
Ovo je vodič za formulu očekivanog povratka. Ovdje smo raspravljali o načinu izračuna očekivanog povrata zajedno s praktičnim primjerima. Kalkulator očekivanog povrata nudimo i za preuzimanje Excel predložak. Možete pogledati i sljedeće članke da biste saznali više -
- Vodič za formulu omjera prihoda od prodaje imovine
- Vodič za ponudu potražite formulu za širenje
- Kako izračunati stopu iskorištenja kapaciteta?
- Proračun ekvivalentnog prinosa obveznice
- Omjer prihoda od prodaje | Primjeri | Predložak Excela