Uvod u hijerarhijski algoritam klasteriranja
Hijerarhijski algoritam klasteriranja je tehnika nenadziranog strojnog učenja. Njegov je cilj pronaći prirodno grupiranje na temelju karakteristika podataka.
Algoritam hijerarhijskog grupiranja ima za cilj pronalaženje ugniježđenih skupina podataka izgradnjom hijerarhije. Slično je s biološkom taksonomijom biljnog ili životinjskog carstva. Hijerarhijski klasteri su općenito predstavljeni pomoću hijerarhijskog stabla poznatog kao dendrogram.
Vrste hijerarhijskog algoritma klastera
Hijerarhijski algoritmi grupiranja su 2 tipa:
- razdvajajući
- aglomerativnim
1. podjele
To je pristup odozgo prema dolje, gdje se u početku cjelokupni podaci smatraju jednom skupinom, a zatim ih iterativno dijeli na podskupine. Ako je poznat broj hijerarhijskog algoritma grupiranja, tada se proces podjele zaustavlja nakon postizanja broja klastera. Inače, proces se zaustavlja kad se podaci više ne mogu podijeliti, što znači da je podskupina dobivena trenutnom iteracijom jednaka onoj dobivenoj iz prethodne iteracije (također se može uzeti u obzir da se podjela zaustavlja kad je svaka točka podataka klaster ).
2. aglomerativni
To je pristup odozdo prema gore koji se oslanja na spajanje klastera. U početku se podaci dijele na m jednotonske klastere (gdje je vrijednost m broj uzoraka / podataka). Dva klastera su spojena u jedan iterativno, čime se smanjuje broj klastera u svakoj iteraciji. Ovaj postupak spajanja klastera prestaje kada su svi klasteri spojeni u jedan ili je postignut broj željenih klastera.
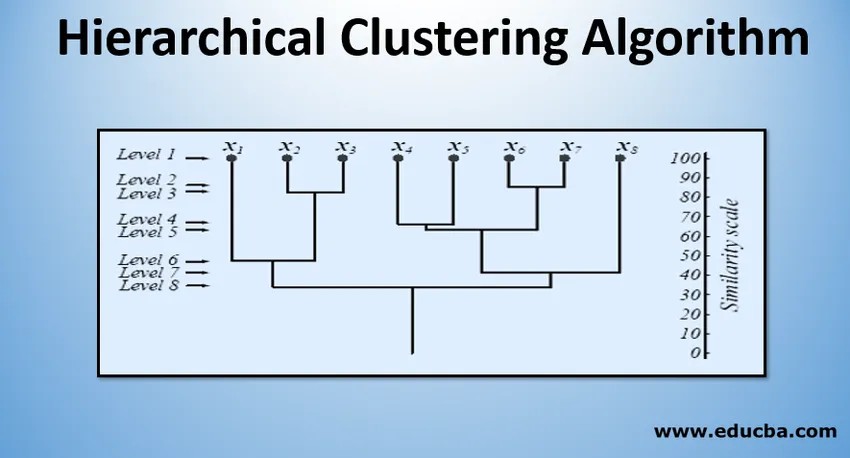
Na razini 1, postoje m klasteri koji se smanjuju na 1 klaster na razini m. One točke podataka koje se spajaju radi formiranja klastera na nižoj razini ostaju u istom klasteru i na višim razinama. Npr., Pretpostavimo da postoji 8 točaka x1..x8, tako da u početku postoji 8 klastera na razini 1. Pretpostavimo da se točke x1 i x2 spoje u klaster na razini 2, a zatim do razine 8, ostaju u istom klasteru.
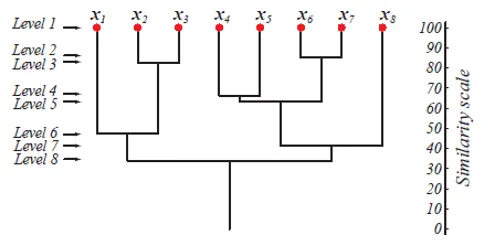
Gornja slika prikazuje dendrogramski prikaz klasteriranja aglomeracije za 8 podatkovnih točaka kao i skala sličnosti koja odgovara svakoj razini.
Razine klastera daju nam predodžbu o tome koliko su slične podatkovne točke u klasterima. Kao što je prikazano na slici 1, ranije se točke podataka spajaju u klaster, slične su. Dakle, podatkovne točke unutar klastera na razini 2 (npr. X2 i x3) sličnije su onima podatkovnih točaka u klasteru na razini 6 (npr. X1 i x2).
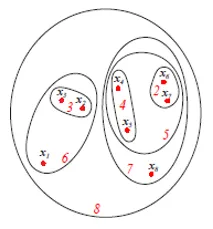
Gornja slika prikazuje skup ili Venn dijagram prikaz aglomerativnog pristupa klastera gore navedenih 8 podataka. Za grupiranje se mogu koristiti i dendrogrami i postavljeni reprezentacije. Međutim, dendrogram je obično poželjno predstavljanje imovine ne može kvantitativno predstaviti sličnosti klastera.
Koraci za hijerarhijski algoritam klasteriranja
Slijedimo sljedeće korake za algoritam hijerarhijskog grupiranja koji su dani u nastavku:
1. Algoritam
Algoritam aglomerativnog hijerarhijskog grupiranja
- Počnite inicijalizirati c, c1 = n, Di = (xi), i = 1, …, n '
- Učinite c1 = c1 - 1
- Pronađite najbliže klastere, recimo, Di i Dj
- Spoji Di i Dj
- Sve dok c = c1
- Povratak c klastera
- Kraj
Ovaj algoritam započinje s n klastera u početku gdje je svaka podatkovna točka klaster. Svakom iteracijom broj klastera smanjuje se za 1 dok se 2 najbliža klastera spajaju. Ovaj se proces nastavlja sve dok se broj klastera ne smanji na unaprijed zadanu vrijednost c.
Kako odlučiti koji su klasteri u blizini?
To se definira pomoću nekoliko metričkih udaljenosti koje su sljedeće:
- Minimalna udaljenost između klastera dmin (Di, Dj). Korisno za samce.
- Maksimalna udaljenost između klastera dmax (Di, Dj). Korisno za cjelovito.
- Prosječna udaljenost između nakupina davg (Di, Dj).
Što je jednostruka i potpuna veza?
- Kad se dmin (di, dj) koristi za pronalazak udaljenosti između dva klastera, a algoritam prestaje ako udaljenost između najbližih klastera prelazi prag, tada se algoritam naziva algoritam jednosmjerne veze.
- Kad se dmax (Di, Dj) koristi za pronalazak udaljenosti između dva klastera, a algoritam prestaje ako udaljenost između najbližih klastera prelazi prag, tada se algoritam naziva algoritam potpune veze.
- Razmotrimo svaku točku podataka kao čvor grafikona. Postoje dvije granice ako pripadaju istom skupu podataka. Kad se dva najbliža grozda spoje, dodaje se rub. Naziva se jednom vezom jer postoji jedinstvena staza od jednog čvora do drugog.
- Algoritam potpune veze spaja dva klastera smanjujući udaljenost između dvije najudaljenije točke.
- Jedan algoritam povezivanja generira opružno stablo. Međutim, ovaj je algoritam osjetljiv na buku. Kompletni algoritam povezivanja generira kompletan graf.
Koja je vremenska složenost algoritma?
Pretpostavimo da u d-dimenzionalnom prostoru imamo n obrazaca, a dmin (Di, Dj) koristimo za formiranje c klastera. Moramo izračunati n (n - 1) udaljenosti među točkama - od kojih je svaka O (d 2 ) proračun - i rezultate staviti u tablicu udaljenosti između točaka. Složenost prostora je O (n 2 ). Pronalaženje para minimalnih udaljenosti (za prvo spajanje) zahtijeva da pređemo cijeli popis, zadržavajući indeks najmanje udaljenosti.
Stoga je za prvi aglomerativni korak složenost O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Za drugi proizvoljni korak aglomeracije (tj. Od c1 do c1 - 1), samo korak kroz n (n - 1) - c1 "neiskorištene" udaljenosti na popisu i pronalazimo najmanju vrijednost za koju x i x 'leže u različitim klasterima, Ovo je, opet, O (n (n-1) -c1). Ukupna vremenska složenost je dakle O (cn 2 d 2 ), a u tipičnim uvjetima n >> c.
2. Vizualizacija
Jednom kada se podaci podijele na klastere, dobra je praksa vizualizirati klastere kako bi se dobila ideja kako skupljanje izgleda. Ali teško je vizualizirati ove podatke velike dimenzije. Stoga koristimo analizu glavnih komponenti (PCA) za vizualizaciju. Nakon PCA, dobivamo podatkovne točke u prostoru malih dimenzija (uglavnom 2D ili 3D) koje možemo zamisliti kako bismo vidjeli grupiranje.
Napomena: Velika dimenzija znači veliki broj značajki, a ne broj podataka.3. Procjena
Jedna od metoda za evaluaciju klastera je da udaljenost točaka između klastera (među-klaster udaljenost) treba biti mnogo veća od udaljenosti točaka unutar klastera (unutar-klaster udaljenost).
Zaključak
Evo nekoliko ključnih postupaka:
- Algoritam hijerarhijskog grupiranja koristi se za pronalaženje ugniježđenih obrazaca u podacima
- Hijerarhijsko grupiranje je 2 tipa - Divisivno i aglomerativno
- Dendrogram i set / Venn dijagram mogu se koristiti za predstavljanje
- Pojedinačna veza spaja dva klastera smanjujući minimalnu udaljenost između njih. Tvori raspon
- Kompletna veza spaja dva grozda minimizirajući maksimalnu udaljenost između nje.
- Ukupna vremenska složenost hijerarhijskog algoritma grupiranja je O (cn 2 d 2 ), gdje je c unaprijed definirani broj klastera, n je broj obrazaca i d je dvodimenzionalni prostor n obrazaca.
Preporučeni članci
Ovo je vodič za algoritam hijerarhijskog klasteriranja. Ovdje ćemo raspravljati o vrstama i koracima algoritama hijerarhijskog grupiranja. Možete pogledati i sljedeće članke da biste saznali više -
- Hijerarhijska analiza klasteriranja
- Hijerarhijsko grupiranje u R '
- Algoritam klastera
- Što je klasteriranje u Rudarstvu podataka?
- Hijerarhijsko grupiranje | Aglomerativno i podjeljeno grupiranje
- C ++ algoritam | Primjeri C ++ algoritma