Ponderirana prosječna formula (Sadržaj)
- Ponderirana prosječna formula
- Kalkulator prosječnog ponderiranog prosjeka
- Ponderirana prosječna formula u Excelu (sa Excelovim predloškom)
Ponderirana prosječna formula
Formula za izračun ponderiranog prosjeka je sljedeća:
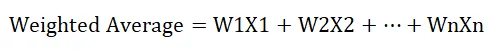
Gdje,
- W označava relativnu težinu (u%)
- X označava vrijednost
Primjeri ponderirane prosječne formule
Pogledajmo nekoliko primjera za razumijevanje ponderirane prosječne formule:
Primjer 1
Pretpostavimo da je Anand uložio novac u slijedeće proporcije: 40% u investiciju A, 20% u investiciju B i 40% u investiciju C. Te investicije imaju stopu povrata kako slijedi: Ulaganje A kao 15%, Ulaganje B kao 10 %, a investicija C 20%. Moramo izračunati ponderirani prosjek za stope povrata koje bi Anand dobio.
Ovdje,
- Za ulaganje A, B i C imamo relativne ponderi od 40%, 20%, odnosno 40%.
- Vrijednost (stopa prinosa) za ulaganja A, BiH kao 15%, 10%, odnosno 20%.
Koristeći ponderiranu prosječnu formulu, dobivamo-
- Ponderirani prosjek = W1 X1 + W2 X2 + …… + Wn Xn
- Ponderirani prosjek = 40% * 15% + 20% * 10% + 40% * 20%
- Ponderirani prosjek = 16%
To pokazuje da će Anand dobiti 16-postotni prosječni povrat od ulaganja A, BiH i C.
Primjer 2
Pretpostavimo da se Anand upisao na tečaj matematike, njegova će se konačna ocjena utvrđivati na osnovu sljedećih kategorija: testovi 30%, završni ispit 40%, kvizovi 15% i domaći zadatak 15%.
Anand je postigao sljedeću ocjenu u svakoj kategoriji: Testovi-80, Završni ispit-65, Kvizovi-85, Domaća zadaća-90. Sada moramo saznati ukupnu ocjenu Ananda.
Da bi se izračunao ponderirani prosjek s postocima, vrijednost svake kategorije prvo treba pomnožiti s njezinim postotkom. Tada se sve te nove vrijednosti moraju zbrajati.
Ovdje,
Imamo sljedeće relativne utege za sljedeće kategorije:
- Testovi 30%
- Završni ispit 40%
- kvizovi 15%
- domaća zadaća 15%
I, vrijednost (ocjene) za kategorije kao
- Testovi-80
- Završni ispit-65,
- testovi-85
- domaće zadaće-90
Koristeći ponderiranu prosječnu formulu, dobivamo-
- Ponderirani prosjek = W1 X1 + W2 X2 + …… + WnXn
- Ponderirani prosjek = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
- Ponderirani prosjek = 76, 25 ili 76%
To pokazuje da je ukupna ocjena Ananda 76%.
Primjer 3
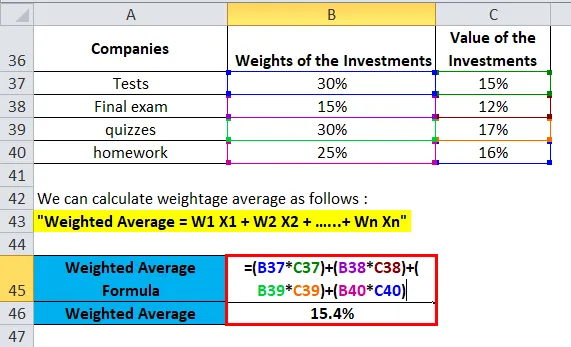
Pretpostavimo da su Jagriti uložili novac u dionice različitih tvrtki. Jagriti portfelj sadrži 30% na zalihama A, 15% na zalihama B, 30% na zalihama C i preostalih 25% na zalihama D. Očekivani prinos prema trenutnoj tržišnoj situaciji na ovim dionicama je sljedeći: Povrat na zalihe A je 15%, povrat na zalihama B je 12%, povrat na zaliha C 17%, a povrat na zalihe D 16%. Jagriti želi izračunati svoj prosječni prinos na portfelju prema trenutnoj situaciji na tržištu.
Ovdje,
- Relativni ponderi dionica u portfelju su sljedeći: A, B, C&D kao 30%, 15%, 30%, odnosno 25%.
- A, vrijednost (stopa prinosa) za zalihe kako slijedi: A, B, C&D kao 15%, 12%, 17%, odnosno 16%.
Koristeći ponderiranu prosječnu formulu, dobivamo-
- Ponderirani prosjek = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
- Ponderirani prosjek = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
- Ponderirani prosjek = 0, 154 ili 15, 4%
To pokazuje da će Jagriti primati 15, 4% prosječnog ponderiranog povrata iz portfelja dionica A, B, C i D.
Objašnjenje ponderirane prosječne formule
Formula ponderiranog prosjeka koristi se za izračunavanje prosječne vrijednosti za određeni skup brojeva s različitim razinama relevantnosti. Utezi moraju biti predstavljeni u ukupnoj relevantnosti kao postotak. Utežene težine trebaju biti jednake 100%, ili 1.
Za izračun prosječne ponderirane formule potrebna nam je relativna težina i vrijednost.
Prva komponenta je relativna težina, a druga komponenta Vrijednosti unosi. Da bismo izračunali ponderirani prosjek, za svaku varijablu uzetu kao vrijednost moramo imati specifičnu vagu, a vaga mora biti jednaka 100%.
Značaj i upotreba ponderirane prosječne formule
Ponderirani prosjek koristi se u raznim financijskim formulama. Nekoliko primjera ponderiranog prosječnog beta i ponderiranog prosječnog troška kapitala (WACC).
Poznati smo s idejom pronalaženja matematičke srednje vrijednosti ili prosjeka za niz predmeta. Jednostavno možemo zbrojiti vrijednosti svih stavki i podijeliti ih s ukupnim brojem predmeta za izračun prosjeka. Ovo će raditi samo ako su svi predmeti jednaki. Na primjer, za izračun prosječnih mjesečnih računa za mobilne uređaje za godinu dana možemo jednostavno zbrojiti ukupne naplaćene iznose za posljednjih dvanaest mjeseci i podijeliti ih sa dvanaest, tada možemo dobiti grubu predodžbu o prosječnom plaćenom računu jer mobilni ciklus računa je otprilike za isto razdoblje, tj. mjesec dana.
Recimo da sada želite izračunati trenutnu prosječnu ocjenu tečaja iz matematike. Obično većina predavanja ispitima daje drugačiju težinu nego domaćim zadacima, internom testu i natjecanjima. U ovom slučaju morate izračunati ponderirani prosjek, koji uzima specifičnu težinu za svaku temu kako biste izračunali ocjenu tečaja.
Primjer nekoliko slučajeva u kojima se mora koristiti ponderirani prosjek umjesto jednostavnog prosjeka. Prvi slučaj- Kada želimo izračunati prosjek koji ima različite postotne vrijednosti za različite kategorije. Gornji primjer ocjene predmeta jedan je od sličnih slučajeva. I drugo kada imamo veliku grupu predmeta s različitom pravilnošću.
Ako tvrtka ima veliku fluktuaciju prodaje zbog proizvodnje sezonskog proizvoda, tada mogu koristiti formulu ponderiranog prosjeka. A tvrtka želi izračunati prosjek za svoje varijabilne troškove, tada tvrtka može koristiti ponderiranu prosječnu formulu i prodaju uzeti kao težinu kako bi bolje razumjela svoje troškove. I mogu usporediti iznos koji proizvode ili prodaju.
Kalkulator prosječnog ponderiranog prosjeka
Možete upotrijebiti sljedeći Kalkulator prosječnog ponderiranog izračuna
| W 1 | |
| X 1 | |
| W 2 | |
| X 2 | |
| W 3 | |
| X 3 | |
| W 4 | |
| X 4 | |
| Ponderirana prosječna formula | |
| Ponderirana prosječna formula = | Š 1 * X 1 + Š 2 * X 2 + Š 3 * X 3 + Š 4 * X 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Ponderirana prosječna formula u Excelu (sa Excelovim predloškom)
Ovdje ćemo napraviti isti primjer formule ponderiranog prosjeka u Excelu. Vrlo je jednostavno i jednostavno. Morate navesti dva ulaza, tj. Relativni utezi i Stopa povrata.
Jednostavno možete izračunati ponderirani prosjek pomoću formule u priloženom predlošku.
prosječni ponder za ponderiranje od ulaganja Investicije A i B izračunava se kao:

ukupna ocjena Ananda izračunava se kao:

težina prosječnih dobitaka iz portfelja dionica A, B, C i D izračunava se kao:
Ovdje možete preuzeti ovaj ponderirani prosječni obrazac Excel predloška ovdje - Ponderirani prosječni obrazac Excel predloška
Preporučeni članci
Ovo je vodič za formulu ponderiranog prosjeka. Ovdje smo raspravljali o njegovoj upotrebi zajedno s praktičnim primjerima. Također vam nudimo kalkulirani prosječni ponderirani predložak Excela za preuzimanje. Možete pogledati i sljedeće članke da biste saznali više -
- Kako izračunati nadzemni omjer?
- Izračunajte pravični multiplikator pomoću primjera
- Uporaba formule bruto dobiti marže
- Vodič za izračun prometa od potraživanja