
Poissonova formula za raspodjelu (Sadržaj)
- Formula
- Primjeri
- Kalkulator
Kakva je formula Poissonove distribucije?
U vjerojatnosti i statistici postoje tri vrste distribucije koje se temelje na kontinuiranim i diskretnim podacima - Normalna, binomna i Poissonova distribucija. Normalna raspodjela često je kao Bell krivulja. Poissonova distribucija često se naziva i Distribucija rijetkih događaja. To se uglavnom koristi za predviđanje vjerojatnosti događaja koji će se dogoditi na temelju toga koliko se često događaj dogodio u prošlosti. Pruža mogućnost određenog broja događaja koji se dešavaju u određenom periodu. Koristi se u mnogim stvarnim situacijama.
Formula za pronalaženje Poissonove distribucije data je u nastavku:
P(x) = (e -λ * λ x) / x!
Za x = 0, 1, 2, 3…
Ovaj eksperiment obično broji broj događaja koji su se dogodili na tom području, udaljenost ili volumen. Uporedo s tim, može se naći Lanac događaja koji nije ništa drugo nego lanac pojava istog događaja tijekom određenog vremenskog razdoblja. Poissonova distribucija ima sljedeće zajedničke karakteristike.
- Događaj se može dogoditi bilo koji broj u bilo koje vrijeme.
- Događaj može uzeti u obzir sve mjere poput volumena, područja, udaljenosti i vremena.
- No vjerojatnost da će se neki događaj dogoditi u bilo kojem od prethodno spomenutih mjera je ista.
- Svaki događaj ne ovisi o svim ostalim događajima što znači da vjerojatnost da se neki događaj ne utječe na druge događaje koji se događaju u isto vrijeme.
Primjeri formule raspodjele Poissona
Uzmimo primjer kako bismo bolje razumjeli izračunavanje Poissonove distribucije.
Možete preuzeti ovaj predložak Excelove formule za distribuciju Poissona ovdje - Poisson distribucijski obrazac Excel predložakFormula raspodjele Poissona - Primjer # 1
Prosječan broj godišnjih nesreća koje se događaju na platformi Željezničke stanice tijekom kretanja vlaka je 7. Da bi se utvrdila vjerojatnost da na ovoj platformi ove godine postoje točno 4 incidenta, može se koristiti Poissonova formula za raspodjelu.
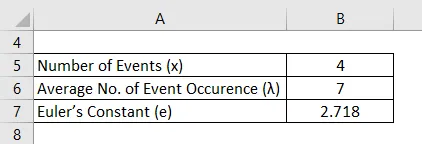
Riješenje:
Poissonova raspodjela izračunava se prema nižoj formuli
P (x) = (e -λ * λ x) / x!
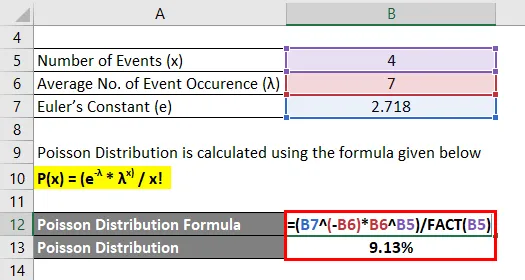
- P (4) = (2.718 -7 * 7 4) / 4!
- P (4) = 9, 13%
Za navedeni primjer, postoji 9, 13% šanse da će se dogoditi točno isti broj nesreća koje se mogu dogoditi ove godine.
Formula raspodjele Poissona - Primjer br. 2
Broj pogrešaka pri tipkanju koje je napisao daktilograf ima distribuciju Poisson. Pogreške su napravljene neovisno pri prosječnoj stopi od 2 po stranici. Pronađite vjerojatnost da pismo s tri stranice ne sadrži pogreške.
Ovdje je prosječna stopa po stranici = 2 i prosječna stopa za 3 stranice (λ) = 6
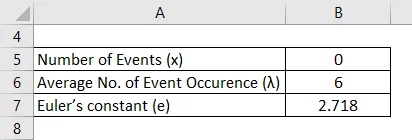
Riješenje:
Poissonova raspodjela izračunava se prema nižoj formuli
P (x) = (e -λ * λ x) / x!
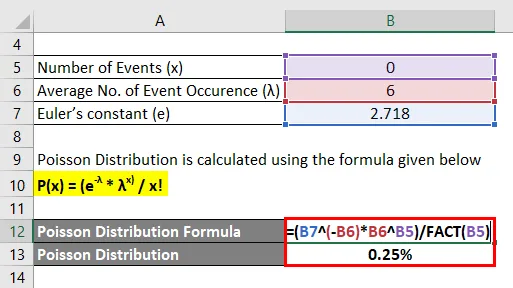
- P (0) = (2.718 -6 * 6 0 ) / 0!
- P (0) = 0, 25%
Dakle, postoji 0, 25% šanse da neće biti pogreške za 3 stranice.
Napomena : x 0 = 1 (svaka vrijednost snage 0 uvijek će biti 1) ; 0! = 1 (nulta fabrika će uvijek biti 1)Obrazloženje
U nastavku je korak po korak pristup izračunavanju Poissonove formule raspodjele.
Korak 1: e je Eulerova konstanta koja je matematička konstanta. Vrijednost e općenito je 2.718 .
2. korak: X je broj stvarnih događaja koji su se zbili. Može imati vrijednosti poput sljedećih. x = 0, 1, 2, 3…
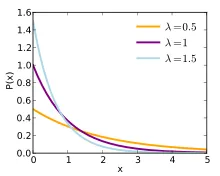
Korak 3: λ je prosječni (prosječni) broj događaja (poznat i kao „parametar raspodjele Poissona“). Ako uzmete jednostavan primjer za izračun λ => 1, 2, 3, 4, 5. Ako u gornjoj formuli primijenite isti skup podataka, n = 5, dakle znači = (1 + 2 + 3 + 4 + 5) / 5 = 3. Za veliki broj podataka ručno pronalaženje medijane nije moguće. Stoga je važno koristiti formulu za veliki broj skupova podataka. Ovdje kod izračunavanja Poissonove distribucije obično ćemo izravno dobiti prosječni broj. Na temelju vrijednosti λ, Poissonov graf može biti unimodalni ili bimodalni kao dolje.
4. korak: x! je Faktor stvarnih događaja dogodio se x. Ispod je primjer kako izračunati faktore za dati broj.
Ako uzmete jednostavan primjer za izračun Faktora stvarnog skupa podataka => 1, 2, 3, 4, 5.
- x! = x * (x-1) * (x-2) * (x-3) * …… 3 * 2 * 1
- 5! = 5 * (5-1) * (5-2) * (5-3) * (5-4)
- 5! = 5 * 4 * 3 * 2 * 1
- 5! = 120
Relevantnost i upotreba formule raspodjele Poissona
Poissonova raspodjela može funkcionirati ako je skup podataka diskretna raspodjela, a svaki je događaj neovisan o ostalim događajima koji se događaju, opisuje diskretne događaje u intervalu, događaji u svakom intervalu mogu se kretati od nule do beskonačnosti i znači da broj događaja mora biti konstantna tijekom cijelog postupka. Ovisno o vrijednosti parametra (λ), raspodjela može biti unimodalna ili bimodalna. Poissonova distribucija je diskretna raspodjela, znači događaj se može naznačiti samo kao događaj ili ne kao događaj, što znači da se broj može navesti samo u cijelim brojevima. Frakcijske pojave događaja nisu dio ovog modela. Rezultati ishoda mogu se klasificirati kao uspjeh ili neuspjeh. To se široko koristi u svijetu:
- Analiza podataka za prediktivnu analizu podataka
- Predviđanja dionica
- Predviđanja tržišta prodaje
- Predviđanja lanca ponude i potražnje
- Lako je dostupan na Amazon Web Services (AWS) platformama
- Pregled i procjena pokrića poslovnog osiguranja
Ostale primjene Poissonove distribucije proizlaze iz otvorenijih problema. Na primjer, može se koristiti za određivanje najmanje potrebne količine resursa u pozivnom centru na temelju prosječnih primljenih poziva i čekanja na čekanju. Ukratko, popis aplikacija može se dodavati sve više i više jer se koristi u svjetskim praktičnim statističkim svrhama.
Kalkulator raspodjele Poissonove formule
Možete koristiti sljedeći Poisson-ov Kalkulator raspodjele
| λ | |
| x | |
| P (X) | |
| P (x) = | (e- λ * λ x ) / x! | |
| (0 -0 * 0 0 ) / 0! = | 0 |
Poissonova formula za distribuciju u Excelu (sa Excelovim predloškom)
Ovdje ćemo napraviti još jedan primjer Poissonove distribucije u Excelu. Vrlo je jednostavno i jednostavno.
Izračunajte Poissonovu raspodjelu u Excelu pomoću funkcije POISSON.DIST.
Ispod je sintaksa formula Poissonove raspodjele u Excelu.

Poissonova distribucija ima sljedeći argument:
Gdje,
- x = broj pojava za koje je potrebno znati vjerojatnost.
- Srednja vrijednost = Prosječan broj pojava u vremenskom razdoblju.
- Kumulativno = Njegova vrijednost bit će Lažna ako nam je potrebna točna pojava događaja i Točno ako će broj slučajnih događaja biti između 0 i tog događaja.

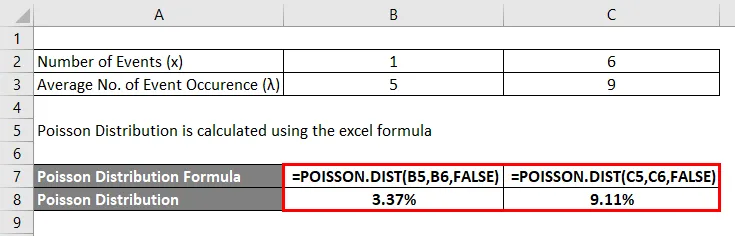
Poissonova raspodjela izračunava se pomoću excelove formule
Preporučeni članci
Ovo je vodič za Poissonovu formulu distribucije. Ovdje ćemo raspraviti kako izračunati Poissonovu raspodjelu zajedno s praktičnim primjerima. Također nudimo Poisson-ov Kalkulator distribucije s mogućnošću skidanja Excel predloška. Možete pogledati i sljedeće članke da biste saznali više -
- Kalkulator za standardnu normalnu formulu raspodjele
- Proračun formule za distribuciju T s predloškom Excel
- Formula za izračun analize varijance
- Što je formula neto vrijednosti imovine?