
Uvod u rekurzivne funkcije u Javi
Rekurzivna funkcija je ona koja sebe poziva jedan ili više puta. Rekurzivna funkcija koristi se u situacijama kada se isti i ponovni postupak moraju izvoditi iznova i iznova dok se rezultat ne postigne. Izvodi nekoliko iteracija i izjava problema postaje pojednostavljena sa svakom ponavljanjem.
Uvijek treba odrediti osnovnu granicu tijekom pisanja rekurzivne funkcije inače rezultira pogreškom prelijevanja snopa. Skup je memorijsko područje rezervirano za održavanje poziva metoda. Pogreška je zbog toga što se funkcija počinje izvršavati u kontinuitetu jer neće moći pronaći ograničavajući uvjet i na kraju iscrpiti dodijeljenu memoriju. Da bismo spriječili prevrtanje Stack-a, definiramo određene osnovne uvjete uz pomoć „if… else“ izraza (ili bilo kojeg drugog uvjetnog iskaza) zbog čega se funkcija rekurzije zaustavlja čim se zahtijeva izračunavanje.
Vrste rekurzije u Javi
Postoje dvije vrste rekurzije na Javi. Oni su:
1. Izravna rekurzija
Sintaksa:
Ovdje se funkcija1 neprestano naziva te je stoga rekurzivna funkcija.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Primjer
Faktor broja je primjer izravne rekurzije. Osnovno načelo rekurzije je rješavanje složenih problema dijeljenjem na manje. Na primjer, u slučaju faktororija broja, izračunamo faktorat "i" ako znamo njegovo faktorije "i-1".
Kodirati:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Izlaz:

2. Neizravna / uzajamna rekurzija
Funkcija1 koja zove drugu funkciju2, a koja zauzvrat poziva funkciju1 bilo izravno ili neizravno, naziva se neizravna rekurzivna funkcija.
Sintaksa:
Razmotrimo 2 funkcije koje se nazivaju function1 () i function2 (). Ovdje funkcija1 poziva funkciju2 i funkciju2 poziva funkciju1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Primjer
Da bismo pokazali neizravnu rekurziju, uzimamo sljedeći program koji se koristi da otkrijemo da li je određeni broj paran ili neparan od datog unosa.
Kodirati:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Izlaz:
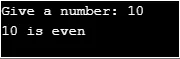
Primjeri rekurzije u Javi
Evo još nekoliko primjera za rješavanje problema pomoću metode rekurzije.
Primjer br. 1 - Fibonaccijeva sekvenca
Kaže se da je skup brojeva "n" u Fibonaccijevom nizu ako je broj 3 = broj1 + broj2, tj. Svaki broj zbroj njegovih prethodnih dva broja. Dakle, slijed uvijek započinje s prve dvije znamenke poput 0 i 1. Treća znamenka zbroj je 0 i 1 što rezultira s 1, četvrti broj je zbrajanje 1 i 1 što rezultira s 2, a slijed nastavlja.
Provjerite sljedeći kod u Javi kako biste generirali Fibonaccijev niz:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Izlaz:

Ovdje se prva dva broja inicijaliziraju u 0 i 1 i ispisuju. Promjenjive vrijednosti "num1", "num2" i "num3" koriste se za generiranje potrebnog slijeda. Promjenjiva „num3“ dobiva se dodavanjem „num1“ i „num2“, a brojevi se pomiču za jedan položaj ulijevo miješanjem, kao što je prikazano u kodu. Ovdje se naziva rekurzivna funkcija "Fibonaccijeva", a pri svakoj se iteraciji vrijednost "n" smanjuje za 1. Dakle, rekurzija izlazi čim "n" dosegne vrijednost 0.
Primjer br. 2 - Hanojska kula
Ovo je klasični matematički problem koji ima 3 pola i "n" broj diskova različite veličine. Zagonetka je sljedeća:
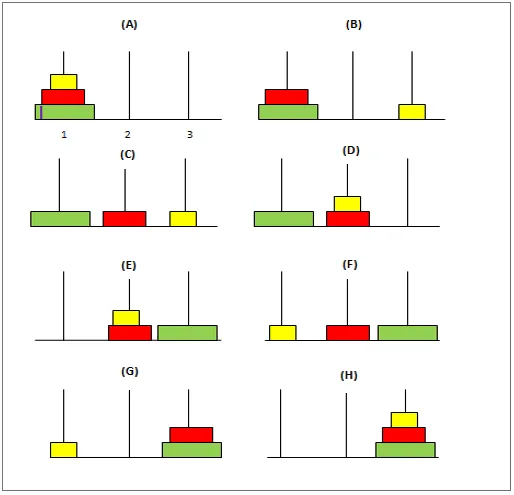
U početku će diskovi biti postavljeni tako da im se najveći disk nalazi na dnu, a najmanji na vrhu stupa. Cilj je pomicanje ovih diskova s prvog pola na treći pol držeći diskove u istom položaju kao u prvom. Slijedi nekoliko uvjeta koje morate imati na umu tijekom izmjene ovih diskova:
1. Istovremeno treba premjestiti samo jedan disk.
2. U tom slučaju postavljanje većeg diska na manji nije dopušteno.
3. Drugi (srednji) stup može se koristiti za posredovanje tijekom prijenosa diskova s prvog na drugi stup.
Slijedi Java kôd koji se može koristiti za rješavanje slagalice:
Kodirati:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Izlaz:
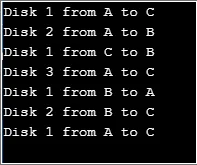
Ovdje varijabla “count” predstavlja broj diskova koji će se koristiti. Funkcija "kula" je rekurzivna funkcija koja se koristi za pomicanje diskova s štapa 1 na šipku 3. Jednostavno rješenje ovog problema može se pružiti razmatranjem najprije 2 diska.
- Prvo započinjemo premještanjem diska1 s štapa 1 na štap 2.
- Zatim premjestimo disk2 na štap 3.
- Konačno, završimo premještanjem diska1 na štap 3 i dovršavanje potrebnog rješenja.
To isto načelo primjenjuje se i za „n“ broj diskova pomicanjem (n-1) diska s palice 1 na 2 i slijedeći slične korake kao gore.
Prednosti rekurzije u Javi
- Kôd se lako piše i održava.
- Najbolja metoda za pronalaženje rezultata gdje je potreban veliki broj ponavljanja.
Nedostaci rekurzije u Javi
- Rekurzivne funkcije koriste više memorije. To je zbog toga što se svaki put poziva rekurzivna funkcija; raspoređivanje memorije vrši se na novo za varijable na snopu. I odgovarajuća dodjela memorije se oslobađa čim se vrate varijable vrijednosti.
- Ovaj postupak dodjele memorije oduzima više vremena, pa je izvršenje obično sporo.
Zaključak
Rekurzivne funkcije se relativno jednostavnije kodiraju, ali također nisu tako učinkovite u usporedbi s ostalim postojećim metodama. Stoga se oni uglavnom koriste u slučajevima kada je vrijeme za razvoj manje, a također i kad se u problemu može primijetiti značajan obrazac.
Preporučeni članci
Ovo je vodič za rekurziju na Javi. Ovdje ćemo raspravljati o vrstama rekurzije u Javi, zajedno s njezinim različitim primjerima s prednostima i nedostacima. Možete pogledati i sljedeće članke da biste saznali više -
- JScrollPane u Javi
- Math funkcije u Javi
- Math funkcije u Javi
- Konstruktor na Javi
- Rekurzivna funkcija u Pythonu
- Faktorski program u JavaScript-u